题目内容
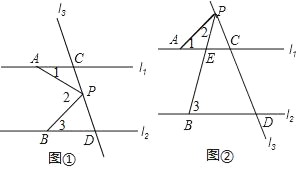
【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
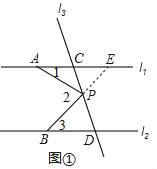
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.
【答案】(1)l1∥l2;(2)∠1+∠2=∠3;理由见解析;(3)∠APB+∠PBD=∠PAC.
【解析】
(1)延长BP交AC于E,则∠2为△APE的外角,所以∠2=∠1+∠AEP,又因为∠2=∠1+∠3,等量代换∠3=∠AEP,根据内错角相等两直线平行,可知l1∥l2,(2)同(1)利用三角形的外角性质及平行线的性质可得∠1+∠2=∠3,(3)过点P作PF∥l1,根据平行于同一条直线的两直线平行,可得PF∥l2,再由平行线的性质进而可得∠APB+∠PBD=∠PAC.
证明:(1)l1∥l2.理由如下,
如图①,延长BP交AC于E,
∵∠2=∠1+∠3,∠2=∠1+∠AEP,
∴∠3=∠AEP,
∴l1∥l2,
故答案为:l1∥l2.
(2)如图②所示,当点P在线段DC的延长线上时,∠1+∠2=∠3,
理由是:∵l1∥l2,
∴∠CEP=∠3
∵∠CEP=∠1+∠2,
∴∠1+∠2=∠3.
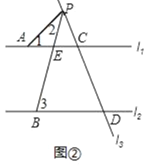
(3)如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠FPA=∠2+∠FPB=∠2+∠3.
即∠APB+∠PBD=∠PAC.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目









