题目内容
【题目】某网店3月份经营一种热销商品，每件成本20元，发现三周内售价在持续提升，销售单价P（元/件）与时间t（天）之间的函数关系为P=30+ 
t（其中1≤t≤21，t为整数），且其日销售量y（件）与时间t（天）的关系如下表
时间t（天） | 1 | 5 | 9 | 13 | 17 | 21 |
日销售量y（件） | 118 | 110 | 102 | 94 | 86 | 78 |
（1）已知y与t之间的变化规律符合一次函数关系，请直接写出y（件）与时间t（天）函数关系式；
（2）在这三周的销售中，第几天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的21天中，该网店每销售一件商品就捐赠a元利润（a＜8）给“精准扶贫”的对象，通过销售记录发现，这21天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．
【答案】
（1）解：设y（件）与时间t（天）函数关系式是y=kt+b，
，得 
，
即y（件）与时间t（天）函数关系式是y=﹣2t+120；
（2）解：设日销售利润为w元，
w=（30+ 
t﹣20）（﹣2t+120）= 
，
∴当t=10时，w取得最大值，此时w=1250，
答：第10天的销售利润最大，最大利润是1250元；
（3）解：设捐赠后的每日的销售利润为w1元，
w1=（30+ t﹣20﹣a）（﹣2t+120）= 
，
∴w1的对称轴是t=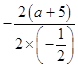 
=2a+10，
∵这21天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，
∴2a+10≥21，
解得，a≥5.5，
又∵a＜8，
∴5.5≤a＜8，
即a的取值范围是5.5≤a＜8．
【解析】（1）根据题意可以设出y（件）与时间t（天）函数关系式，然后根据表格中的数据即可解答本题；（2）根据题意可以得到利润与t的函数关系式，然后化为顶点式即可解答本题；（3）根据题意可以得到相应的函数解析式，然后根据二次函数的性质即可解答本题．
