题目内容
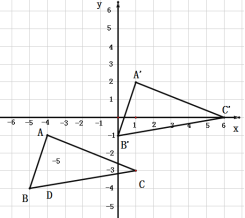
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),将△ABC向右平移5个单位长度,再向上平移3个单位长度得到△![]() ,其中点
,其中点 ![]() 分别是点A,B,C的对应点.
分别是点A,B,C的对应点.
(1)请你在给出的坐标系中画出![]() 和写出点A′,C′的坐标;
和写出点A′,C′的坐标;
(2)若△ABC内的一点P经过上述平移后的对应点为![]() ,用含
,用含![]() 的式子表示P点的坐标 ;(直接写出结果即可)
的式子表示P点的坐标 ;(直接写出结果即可)
(3)求△ABC的面积.

【答案】(1)图详见解析,A′(1, 2),C′(6, 0);(2)P(![]() );(3)8.5.
);(3)8.5.
【解析】
(1)根据平移规律,坐标的平移规律与图形的平移规律相同,将三个顶点坐标分别进行平移得到对应点的坐标,然后依次连线,写出点的坐标即可.
(2)根据坐标的平移规律,用平移后的点按照相反的方向进行平移,即可找到平移前的对应点.
(3)利用割补法,将三角形补成矩形,然后用矩形面积分别减去其它三角形的面积即可得到三角形ABC的面积.
解:(1)根据坐标平移规律,分别将A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),向右平移5个单位长度,再向上平移3个单位长度,![]()
![]() ,依次连线即可.
,依次连线即可.
即![]()
![]()
(2)△ABC内的一点P经过上述平移后的对应点为![]() ,其平移规律为向右平移5个单位长度,再向上平移3个单位长度,所以要求P点坐标,要按照相反的方向平移,即向左平移5个单位长度,再向下平移3个单位长度,即P点坐标为(
,其平移规律为向右平移5个单位长度,再向上平移3个单位长度,所以要求P点坐标,要按照相反的方向平移,即向左平移5个单位长度,再向下平移3个单位长度,即P点坐标为(![]() )
)
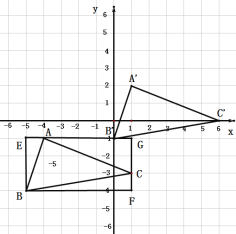
(3)如图,将△ABC补成矩形BEGF,
![]()

 名校课堂系列答案
名校课堂系列答案【题目】问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:在函数y=|x|﹣2中,自变量x可以是任意实数;
Ⅰ如表是y与x的几组对应值.
y | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
x | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
Ⅱ如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:
①该函数的最小值为 ;
②该函数的另一条性质是 .