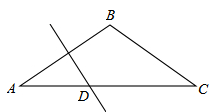
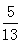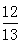题目内容
.如图,已知直线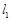 ∥
∥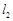 ∥
∥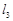 ∥
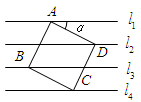
∥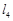 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则
,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则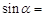 ________.
________.
 ∥
∥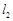 ∥
∥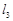 ∥
∥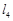 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则
,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则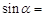 ________.
________.

试题分析:过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵AD=CD,∠AED=∠DFC=90°,
∴△ADE≌△DFC,
∴DE=CF=1,
∴在Rt△CDF中,CD=
 ,
,∴sinα=sin∠CDF=

考点:(1)锐角三角函数的定义;(2)平行线之间的距离;(3)全等三角形的判定与性质;(4)正方形的性质.

练习册系列答案
相关题目
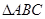 中,
中, ,
,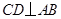 于
于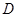 ,
, ,若
,若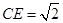 ,
,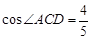 ,求
,求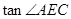 的值及CD的长.
的值及CD的长.
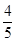 .
.

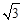 m
m m
m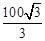 m
m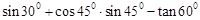 .
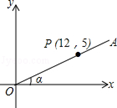
.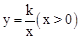 的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=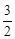 。
。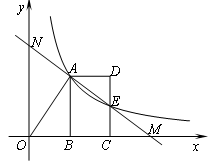
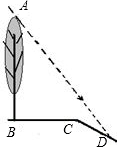
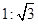 ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是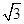 米,则小树AB的高是 米.
米,则小树AB的高是 米.