题目内容
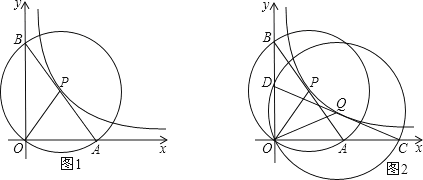
【题目】如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=![]() (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数y=![]() (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
【答案】(1)证明见解析;(2)24;(3)证明见解析.
【解析】
试题分析:(1)∠AOB=90°,由圆周角定理的推论,可以证明AB是⊙P的直径;
(2)将△AOB的面积用含点P坐标的表达式表示出来,容易计算出结果;
(3)对于反比例函数上另外一点Q,⊙Q与坐标轴所形成的△COD的面积,依然不变,与△AOB的面积相等.
试题解析:(1)证明:∵∠AOB=90°,且∠AOB是⊙P中弦AB所对的圆周角,
∴AB是⊙P的直径.
(2)解:设点P坐标为(m,n)(m>0,n>0),
∵点P是反比例函数y=![]() (x>0)图象上一点,
(x>0)图象上一点,
∴mn=12.
如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,则OM=m,ON=n.
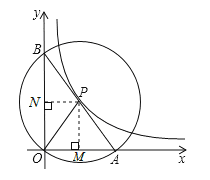
由垂径定理可知,点M为OA中点,点N为OB中点,
∴OA=2OM=2m,OB=2ON=2n,
∴S△AOB=![]() BOOA=
BOOA=![]() ×2n×2m=2mn=2×12=24.
×2n×2m=2mn=2×12=24.
(3)证明:∵以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,∠COD=90°,
∴DC是⊙Q的直径.
若点Q为反比例函数y=![]() (x>0)图象上异于点P的另一点,
(x>0)图象上异于点P的另一点,
参照(2),同理可得:S△COD=![]() DOCO=24,
DOCO=24,
则有:S△COD=S△AOB=24,即![]() BOOA=
BOOA=![]() DOCO,
DOCO,
∴DOOC=BOOA.

练习册系列答案
相关题目