题目内容
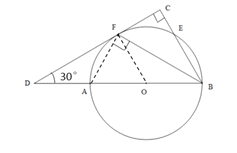
【题目】(满分10分)如图,直径为AB的⊙O交![]() 的两条直角边BC、CD于点E、F,且
的两条直角边BC、CD于点E、F,且![]() ,连接BF.
,连接BF.
(1)求证CD为⊙O的切线;(2)当CF=1且∠D=30°时,求AD长.

【答案】(1) 证明见解析;(2) ![]() .
.
【解析】试题分析:(1)连接OF,只要证明OF∥BC,即可推出OF⊥CD,由此即可解决问题.
(2)连接AF.思想在Rt△BCF中,求出BC,再在Rt△DBC中,求出DB,在Rt△ABF中,求出AB,根据AD=DB-AB即可解决问题.
试题解析:
(1)连接OF.
∵AF=EF ,∴∠CBF=∠FBA.
∵OF=OB,∴∠FBO=∠OFB .
∵点A、O、B三点共线,
∴∠CBF=∠OFB.
∴BC∥OF,∴∠OFC+∠C=180°.
∵∠C=90°,∴∠OFC=90°,即OF⊥DC.
∴CD为⊙O的切线.
(2) ∵∠D=30°,∴∠CBD=60°
∵AF=EF,∴∠CBF=∠DBF=![]() ∠CBD=30°
∠CBD=30°
在![]() , ∵FC=1,∠CBF=30°,∴BF=2CF=2.
, ∵FC=1,∠CBF=30°,∴BF=2CF=2.
∴![]()
连接AF.
∵AB是⊙O的直径,∴∠AFB=90°
在![]() ,∵∠ABF=30°,BF=2,∴AF=
,∵∠ABF=30°,BF=2,∴AF=![]() AB.
AB.
∴AB2=(![]() AB)2+BF2,即
AB)2+BF2,即![]() AB2=4,
AB2=4, ![]()
在![]() ,∵∠D=30°,BC=
,∵∠D=30°,BC=![]() ,∴BD=2BC=
,∴BD=2BC=![]() .
.
∴AD=DB-AB=2![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目