题目内容
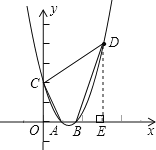
【题目】已知在平面直角坐标系中，点C（0，2），D（3，4），在x轴正半轴上有一点A，且它到原点的距离为1．
（1）求过点C、A、D的抛物线的解析式；
（2）设（1）中抛物线与x轴的另一个交点为B，求四边形CABD的面积；
（3）把（1）中的抛物线先向左平移一个单位，再向上或向下平移多少个单位能使抛物线与直线AD只有一个交点？
【答案】（1）y＝
；（2）S四边形CABD＝5；（3）抛物线y＝
x向下平移
个单位，与直线AD只有一个交点．
【解析】
（1）将A,C,D三点坐标代入，用待定系数法求抛物线的解析式即可.
（2）可以先将B点坐标求出来，然后作DE⊥x轴于点E，则S四边形CABD＝S梯形OEDC﹣S△AOC﹣S△BDE
（3）用待定系数法求出直线AD的解析式，然后将抛物线平移后的解析式设出来，联立之后利用根的判别式为0即可求出.
（1）根据题意可知A的坐标为（1，0），
设过C、A、D三点的抛物线的解析式为：y＝ax2+bx+c（a≠0），
∵C（0，2），A（1，0），D（3，4），
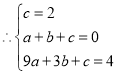
解得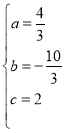
，
故过C、A、D三点的抛物线的解析式为：y＝
（2）∵点B为抛物线与x轴的另一个交点，令y＝0，
则
∴x1＝1，x2＝
，
∴点B的坐标为
，
作DE⊥x轴于点E，
∴S四边形CABD＝S梯形OEDC﹣S△AOC﹣S△BDE＝
（3）把抛物线y＝，
即y＝
，
向左平移一个单位得到的抛物线的解析式为：y＝
，
即y＝
，
设抛物线y＝向上或向下平移|k|个单位能使抛物线与直线AD只有一个交点，
则向上或向下平移|k|个单位抛物线的解析式为：y＝
，
设过A、D两点的解析式为y＝ax+b，
∵A（1，0），D（3，4），
代入上式得
，
解得
，
∴直线AD的解析式为：y＝2x﹣2，
得
，
∴4x2﹣8x+3k+6＝0，
∴△＝64﹣16（3k+6）＝0，
解得，k＝﹣，
即抛物线y＝向下平移个单位，与直线AD只有一个交点．
