题目内容
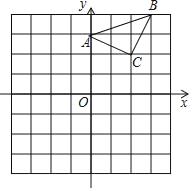
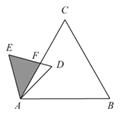
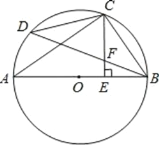
【题目】如图,AB 是⊙O 的直径,C 是![]() 的中点,CE⊥AB 于点 E,BD 交CE 于点 F.
的中点,CE⊥AB 于点 E,BD 交CE 于点 F.
(1)求证:CF=BF;
(2)若 CD=6,AC=8,求⊙O 的半径及 CE 的长.
【答案】(1)见解析;(2) ⊙O 的半径为 5, CE=![]() .
.
【解析】
(1)要证明 CF=BF,可以证明∠1=∠2;AB 是⊙O 的直径,则∠ACB=90°,又知 CE⊥AB,则∠CEB=90°,则∠2=90°﹣∠ACE=∠A,∠1=∠A,则∠1=∠2;
(2)在直角三角形 ACB 中,AB2=AC2+BC2,又知,BC=CD,所以可以求得AB 的长,即可求得圆的半径;再根据三角形相似可以求得 CE 的长.
(1)证明:∵AB 是⊙O 的直径,
∴∠ACB=90°,∴∠A=90°﹣∠ABC.
∵CE⊥AB,∴∠CEB=90°,
∴∠ECB=90°﹣∠AB C,∴∠ECB=∠A.(2 分)又∵C 是![]() 的中点,
的中点,
∴![]() =
= ![]() ,
,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵![]() =
= ![]() ,
,
∴BC=CD=6,
∵∠ACB=90°,
∴AB=![]() =10,
=10,
∴⊙O 的半径为 5,
∵S△ABC= ![]() ABCE=
ABCE= ![]() BCAC,
BCAC,
∴CE= ![]() =
=![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某市篮球队到市一中选拔一名队员,教练对王亮和李刚两名同学进行![]() 次
次![]() 分投篮测试,一人每次投
分投篮测试,一人每次投![]() 个球,下图记录的是这两名同学
个球,下图记录的是这两名同学![]() 次投篮中所投中的个数.
次投篮中所投中的个数.
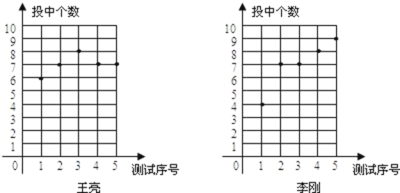
(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 |
| ||
李刚 |
|
|
|
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.