题目内容
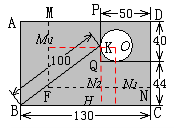
一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上。木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线NF-FM(NF∥BC,FM∥AB)切割,如图1所示。图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则CN,AM的长分别是 .
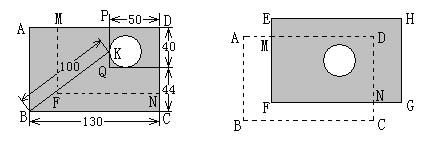

18cm, 31cm。
作辅助线如图所示,设圆孔半径为r,
根据勾股定理,得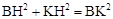 。
。
∴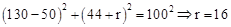 。
。
按题意要求,切割后,以圆O为中心,到两对边的距离相等,
即: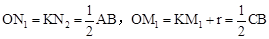 。
。
∵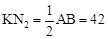 ,∴ QN2+r=42,即QN2=42-16=26。
,∴ QN2+r=42,即QN2=42-16=26。
∴CN=QH-QN2=44-26=18。
又∵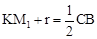 ,即
,即 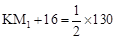 ,∴ KM1=49。
,∴ KM1=49。
∴AM=BC-PD-KM1=130-50-49=31。
∴CN=18cm,AM=31cm。

根据勾股定理,得
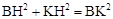 。
。∴
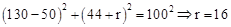 。
。按题意要求,切割后,以圆O为中心,到两对边的距离相等,
即:
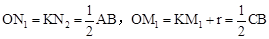 。
。∵
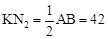 ,∴ QN2+r=42,即QN2=42-16=26。
,∴ QN2+r=42,即QN2=42-16=26。∴CN=QH-QN2=44-26=18。
又∵
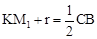 ,即
,即 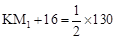 ,∴ KM1=49。
,∴ KM1=49。∴AM=BC-PD-KM1=130-50-49=31。
∴CN=18cm,AM=31cm。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
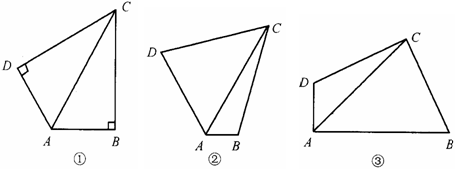
 中,对角线
中,对角线 平分
平分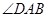 .
.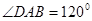 ,
,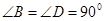 时,求证:
时,求证: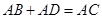 ;
;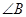 与
与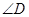 互补时,线段
互补时,线段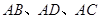 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;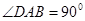 ,
,
 的中点.
的中点.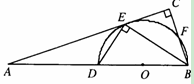
 ,求BC的长.
,求BC的长.