题目内容
【题目】已知,如图,在矩形ABCD中,AB=8,BC=x(0<x≤8),点E在边CD上,且CE=CB,以AE为对角线作正方形AGEF.设正方形AGEF的面积y.
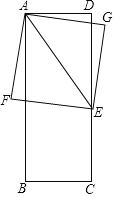
(1)当点F在矩形ABCD的边上时,x= .
(2)求y与x的函数关系式及y的取值范围.
(3)当矩形ABCD的一条边将正方形AGEF的面积分为1:3两部分时,直接写出x的值.
【答案】(1)4;(2)y=x2﹣8x+32=(x﹣4)2+16,16≤y≤32;(3)满足条件的x的值为2或6.
【解析】
(1)点F在矩形ABCD的边上时,AF=EF=FG=BC,利用正方形的性质解决问题即可.
(2)根据y=![]() AE2=
AE2=![]() (AD2+DE2),计算即可.
(AD2+DE2),计算即可.
(3)分两种情形:①如图1中,设CD交AG于Q,当AQ=GQ时,长方形ABCD的边CD将正方形AFEG的面积分成1:3两部分.②如图2中,设AD交EG于Q,当GQ=EG时,长方形ABCD的边AD将正方形AFEG的面积分成1:3两部分.
解:(1)点F在矩形ABCD的边上时,AF=EF=FG=BC,
∵EC=BC,
∴AF=FB=4,
∴BC=EC=BF=4,
故答案为4.
(2)y=![]() AE2=
AE2=![]() (AD2+DE2)=
(AD2+DE2)=![]() [x2+(8﹣x)2]=x2﹣8x+32=(x﹣4)2+16.
[x2+(8﹣x)2]=x2﹣8x+32=(x﹣4)2+16.
∵0<x≤8,
∴16≤y≤32.
(3)①如图1中,设CD交AG于Q,当AQ=GQ时,长方形ABCD的边CD将正方形AFEG的面积分成1:3两部分.
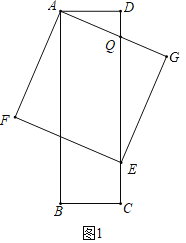
则∵tan∠QEG=tan∠QAD,
∴![]() =
=![]() =
=![]() ,
,
∵AD=BC=x,
∴DQ=![]() x,AQ=GQ=
x,AQ=GQ=![]() xEG=
xEG=![]() x,
x,
∴EQ=![]() x,
x,
∵DQ+QE+CE=8,
∴![]() x+
x+![]() x+x=8,
x+x=8,
∴x=2.
②如图2中,设AD交EG于Q,当GQ=EG时,长方形ABCD的边AD将正方形AFEG的面积分成1:3两部分.
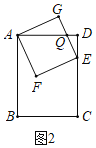
设DQ=m,同法可得DE=2m,QE=GQ=![]() m,AQ=5m,
m,AQ=5m,
∴6m=x,
∴DE=![]() ,
,
∵DE+CE=8,
∴![]() x+x=8,
x+x=8,
∴x=6,
∴满足条件的x的值为2或6.