题目内容
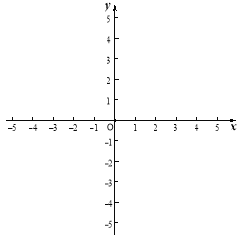
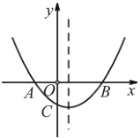
【题目】已知抛物线
的部分图象如图所示，若
，则
的取值范围是（ ）
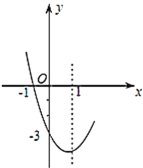
A.
B.
C.
D.
【答案】D
【解析】
利用对称性得到抛物线与x轴的另一个交点坐标为（3，0），再利用待定系数法确定抛物线的解析式为y＝x22x3，接着根据二次函数的性质得到x＝1时，y有最小值4，从而得到当1＜x＜2时对应的y的取值范围．
解：∵抛物线的对称轴为直线x＝1，抛物线与x轴的一个交点坐标为（1，0），
∴抛物线与x轴的另一个交点坐标为（3，0），
∴抛物线的解析式可设为y＝a（x＋1）（x3），
把（0，3）代入得3＝a1（3），解得a＝1，
∴抛物线的解析式为y＝（x＋1）（x3），即y＝x22x3，
∵y＝（x1）24，
∴x＝1时，y有最小值4，
∵x＝2时，y＝x22x3＝3，
∴当1＜x＜2，y的取值范围是4≤y＜0．
故选：D．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本数量少的有
本，最多的有
本，并根据调查结果绘制了不完整的图表，如下所示：
本数（本） | 频数（人数） | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（
）统计图表中的
__________，
__________，
__________．
（
）请将频数分布直方图补充完整．
（
）求所有被调查学生课外阅读的平均本数．
（
）若该校八年级共有
名学生，请你估计该校八年级学生课外阅读
本及以上的人数．
