Question

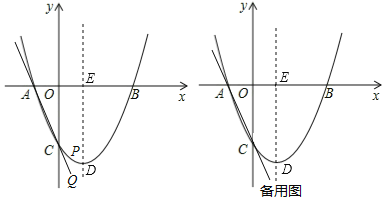
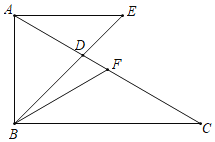
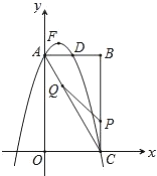
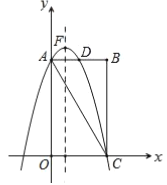
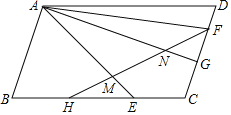
【题目】如图，在平行四边形ABCD中，点H，E在BC边上，点G，F在CD边上，连接AF，AG，AE，HF，AG垂直平分CF，HF分别交AE，AG于点M，N，∠AEB＝45°，∠FHC＝∠GAE．

（1）若AF＝，tan∠FAG＝，求AN；

（2）若∠FHC＝2∠FAG，求证：AE＝MN+BE．

Answer 1

【答案】（1）AN＝3；（2）证明见解析.

【解析】

（1）首先证明△FNG是等腰直角三角形，设FG＝x，则AG＝4k，利用勾股定理求出x即可解决问题．

（2）连接AH，AC．作AK⊥AE交CB速度延长线于K．设AC交FH于O．利用全等三角形的性质证明NM＝BK即可解决问题．

（1）解：∵∠MHE＝∠MAN，∠EMH＝∠AMN，

∴∠ANM＝∠MEH＝45°，

∴∠FNG＝∠ANM＝45°，

∵AG⊥CF，

∴∠AGF＝90°，

∴∠GNF＝∠GFN＝45°，

∴GN＝GF，设GN＝GF＝x，

∵tan∠FAG＝，

∴AG＝4x，

∵AF2＝AG2+FG2，

∴34＝（4x）2+x2，

∴x＝或﹣（舍弃），

∴AN＝3x＝3．

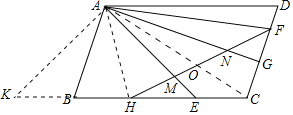
（2）证明：连接AH，AC．作AK⊥AE交CB速度延长线于K．设AC交FH于O．

∵∠KAE＝90°，∠AEK＝45°，

∴∠K＝∠AEK＝45°，

∵AG垂直平分线段CF，

∴AC＝AF，

∴∠GAC＝∠GAF，∠ACF＝∠AFC，

∵∠FHC＝2∠FAG，∠FAC＝2∠FAG，

∴∠FHC＝∠FAC，

∴A，H，C，F四点共圆，

∴∠AHK＝∠AFC，∠AHN＝∠ACF，

∴∠AHK＝∠AHN，

∵∠K＝∠ANH＝45°，AH＝AH，

∴△AHK≌△AHN（AAS），

∴AK＝AN，

∵AB∥CD，AG⊥CD，

∴AG⊥AB，

∴∠GAB＝∠KAE＝90°，

∴∠KAB＝∠NAM，

∴△KAB≌△NAM（ASA），

∴BK＝MN，

∴BE+MN＝BE+BK＝EK＝AE，

即AE＝BE+MN．