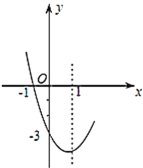题目内容
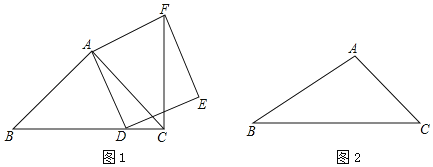
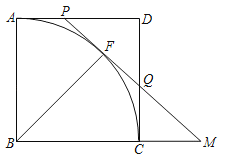
【题目】如图,在边长为5的正方形中,以B为圆心,BA为半径作弧AC,F为弧AC上一动点,过点F作⊙B的切线交AD于点P,交DC于点Q.
(1)求证:PQ=AP+CQ;
(2)分别延长PQ、BC,延长线相交于点M,如果AP=2,求BM的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用切线长定理得到PA=PF,QF=QC,从而得到PQ=PF+QF=AP+CQ;
(2)设CQ=x,则PD=3,PQ=2+x,DQ=5﹣x,利用勾股定理得到32+(5﹣x)2=(2+x)2,解得x=![]() ,则DQ=5﹣x=
,则DQ=5﹣x=![]() ,然后证明△CQM∽△DQP,利用相似比求出CM即可得到BM的长.
,然后证明△CQM∽△DQP,利用相似比求出CM即可得到BM的长.
(1)证明:∵四边形ABCD为正方形,
∴∠BAD=∠BCD=90°,DA=DC,
∵⊙B的切线交AD于点P,
∴PA=PF,QF=QC,
∴PQ=PF+QF=AP+CQ;
(2)解:设CQ=x,
∵AP=2,AD=CD=5,
∴PD=3,PQ=2+x,DQ=5﹣x,
在Rt△PQD中,32+(5﹣x)2=(2+x)2,解得x=![]() ,
,
∴DQ=5﹣x=![]() ,
,
∵PD∥CM,
∴△CQM∽△DQP,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CM=
,解得CM=![]() ,
,
∴BM=BC+CM=5+![]() =
=![]() .
.

【题目】坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设.洛宁县某村出售特色水果(苹果).规定如下:
品种 | 购买数量低于50箱 | 购买数量不低于50箱 |
新红星 | 原价销售 | 以八折销售 |
红富士 | 原价销售 | 以九折销售 |
如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元.
(1)每箱新红星、红富士的单价各多少元?
(2)某单位需要购置这两种苹果120箱,其中红富士的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由.
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
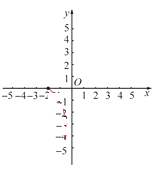
(4)结合函数的图象,写出该函数的一条性质: .