题目内容
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

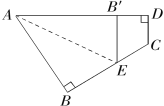
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
【答案】操作一(1) 14cm (2) 35° 操作二 CD=4.5
【解析】
试题:操作一利用对称找准相等的量:BD=AD,∠BAD=∠B,然后分别利用周长及三角形的内角和可求得答案;
操作二 利用折叠找着AC=AE,利用勾股定理列式求出AB,设CD=x,表示出BD,AE,在Rt△BDE中,利用勾股定理可得答案;
试题解析:操作一:
(1)由折叠的性质可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:
7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=9cm,BC=12cm,
∴AB=![]() (cm),
(cm),
根据折叠性质可得AC=AE=9cm,
∴BE=AB-AE=6cm,
设CD=x,则BD=12-x,DE=x,
在Rt△BDE中,由题意可得方程x2+62=(12-x)2,
解之得x=4.5,
∴CD=4.5cm.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】某公司销售一种进价为![]() 元/个的计算器,其销售量
元/个的计算器,其销售量![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的变化如下表:
(元/个)的变化如下表:
价格 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
同时,销售过程中的其他开支(不含造价)总计![]() 万元.
万元.
(![]() )观察并分析表中的
)观察并分析表中的![]() 与
与![]() 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出
之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出![]() (万个)与
(万个)与![]() (元/个)的函数解析式.
(元/个)的函数解析式.
(![]() )求出该公司销售这种计算器的净得利润
)求出该公司销售这种计算器的净得利润![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(![]() )该公司要求净得利润不能低于
)该公司要求净得利润不能低于![]() 万元,请写出销售价格
万元,请写出销售价格![]() (元/个)的取值范围.
(元/个)的取值范围.