Question

【题目】某公司销售一种进价为元/个的计算器，其销售量（万个）与销售价格（元/个）的变化如下表：

价格（元/个）
销售量（万个）

同时，销售过程中的其他开支（不含造价）总计万元．

（）观察并分析表中的与之间的对应关系，用所学过的一次函数，反比例函数或二次函数的有关知识写出（万个）与（元/个）的函数解析式．

（）求出该公司销售这种计算器的净得利润（万个）与销售价格（元/个）的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？

（）该公司要求净得利润不能低于万元，请写出销售价格（元/个）的取值范围．

Answer 1

【答案】（1）；（2）将销售价格定为50元/个时，利润最大为50万元；（3）．

【解析】试题分析：

（1）观察、分析表格中的数据可知，当售价每增加10元时，销售量都是减少1万个，因此与之间的函数关系是一次函数，由此可设，代入表格中的两组对应数据解出k、b即可得所求函数解析式；

（2）由净利润=销售收入-进货成本-其它开支，结合（1）中所得结果和已知即可列出函数关系式；把所得函数关系式配方化为“顶点式”即可得到所求的定价和最大利润；

（3）由（2）中所得解析式结合可解得对应的的值，再结合（2）中所得函数的图象开口向下，即可得到对应的的取值范围.

试题解析：

解：（）根据表格数据： 与为一次函数，设解析式，

，解得，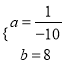

∴解析式： ．

（）由题意得，

化简得，

故将销售价格定为元/个时，利润最大为万元．

（）当利润为万元时， ，解得， ，

∵函数的图象开口向下，

∴当利润不低于40万元时，销售价格的取值范围为．