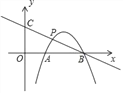
题目内容
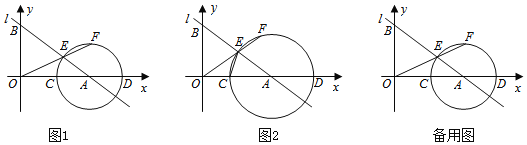
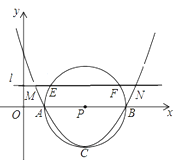
【题目】如图,已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥ x轴,交该抛物线于M、N两点,交⊙ P与E、F两点,若EF=2![]() ,则MN的长是_____.
,则MN的长是_____.
【答案】![]()
【解析】根据题意求出抛物线与x轴交点坐标,以及顶点坐标,进而得出m的值,再利用勾股定理得出M点纵坐标,即可得出MN的长.
过点P作PH⊥MN于点H,连接EP,
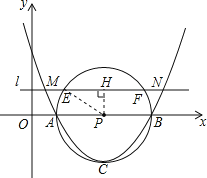
∵y=mx2-6mx+5m=m(x-1)(x-5),
∴抛物线与x轴的交点坐标A(1,0),B(5,0),
∵y=mx2-6mx+5m=m(x-3)2-4m,
∴C(3,-4m),P(3,0),
故⊙P的半径为4m,
则AP=4m,
可得:OP=3=1+4m,
解得:m=![]() ,
,
∴AP=EP=2,
∵PH⊥MN,
∴MH=HN=![]() ,
,
∴PH=1,
当y=1,则1=![]() (x-1)(x-5),
(x-1)(x-5),
整理得:x2-6x+3=0,
解得:x1=3-![]() ,x2=3+
,x2=3+![]() ,
,
故MN=3+![]() -(3-
-(3-![]() )=2
)=2![]() .
.
故答案为:2![]() .
.

练习册系列答案
相关题目