Question

【题目】如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（　　）

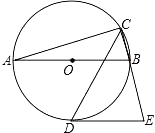
A. B. 2 C. D.

Answer 1

【答案】C

【解析】如图连接OC、OD，CD与AB交于点F．

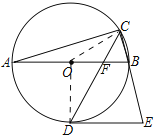
∵AB是直径，

∴∠ACB=90°，

∵CD平分∠ACB，

∴ ，

∴OD⊥AB，

∵DE是切⊙O切线，

∴DE⊥OD，

∴AB∥DE，∵∠E=75°，

∴∠ABC=∠E=75°，∠CAB=15°，

∴∠CFB=∠CAB+∠ACF=15°+45°=60°，

∴∠OFD=∠CFB=60°，

在RT△OFD中，∵∠DOF=90°，OD=2，∠ODF=30°，

∴OF=ODtan30°=，DF=2OF=，

∵OD=OC，

∴∠ODC=∠OCD=30°，

∵∠COB=∠CAB+∠ACO=30°，

∴∠FOC=∠FCO，

∴CF=FO=，

∴CD=CF+DF=，

故选C．