题目内容
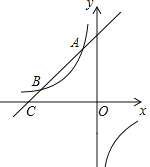
【题目】如图,一次函数y=x+b的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(1)求一次函数和反比例函数的表达式;
(2)若点D是第四象限内反比例函数图象上的点,且点D到直线AC的距离为5![]() ,求点D的横坐标.
,求点D的横坐标.
【答案】(1)y=x+4;y=﹣![]() ;(2)点D的横坐标x=±
;(2)点D的横坐标x=±![]() +3.
+3.
【解析】
(1)将点C坐标代入y=x+b可得其解析式,将A的坐标代入一次函数和反比例函数解析式可得k的值,从而得出反比例函数解析式;
(2)过点D作DE∥AC交x轴于点E,过点E作EF⊥AC于点F,设直线DE的解析式为y=x+m,EF=5![]() ,由题意得出CO=GO=4知CE=
,由题意得出CO=GO=4知CE=![]() EF=10,EO=6,从而得E(6,0),将E(6,0)代入y=x+m中得m=﹣6,从而得出y=x﹣6,联立
EF=10,EO=6,从而得E(6,0),将E(6,0)代入y=x+m中得m=﹣6,从而得出y=x﹣6,联立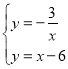 解之可得答案.
解之可得答案.
解:(1)将C(﹣4,0)代入y=x+b,得b=4,
∴一次函数的表达式为y=x+4,
将A(﹣1,a)代入y=x+4,y=![]() 中,得:a=﹣1+4,a=
中,得:a=﹣1+4,a=![]() ,
,
∴k=﹣3,
∴反比例函数的表达式为y=﹣![]() ;
;
(2)过点D作DE∥AC交x轴于点E,过点E作EF⊥AC于点F,
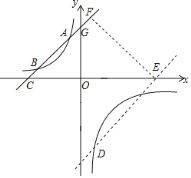
∴设直线DE的解析式为y=x+m,EF=5![]() ,
,
∵y=x+4,x=0时,y=4,
∴G(0,4),
又C(﹣4,0),
∴CO=GO=4,
又∠GOC=90°,
∴∠GCO=45°,
又∵EF⊥AC,
∴CE=![]() EF=10,
EF=10,
∴EO=EC-CO=6,
∴E(6,0),
将E(6,0)代入y=x+m中,得:m=﹣6,
∴y=x﹣6,
联立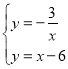 ,
,
解得x=![]() +3,
+3,
∴点D的横坐标为![]() +3或-
+3或-![]() +3.
+3.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?