题目内容
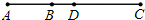如图所示，点C在线段AB的延长线上，且BC=2AB，D是AC的中点，若AB=2cm，求BD的长．
解：∵AB=2cm，BC=2AB，
∴BC=4cm．
∴AC=AB+________=________cm．
∵D是AC的中点，
∴AD=
________=________cm．
∴BD=AD-________=________cm．
BC 6 AC 3 AB 1
分析：求出BC长，根据线段中点求出AD，代入BD=AD-AB求出即可．
解答：∵AB=2cm，BC=2AB，
∴BC=4cm，
∴AC=AB+BC=6cm，
∵D为AC中点，
∴AD=AC=3cm，
∴BD=AD-AB=3cm-2cm=1cm，
故答案为：BC，6，AC，3，AB，1．
点评：本题考查了线段中点和求两点间的距离的应用，关键是求出AC、AD长和得出BD=AD-AB．
分析：求出BC长，根据线段中点求出AD，代入BD=AD-AB求出即可．
解答：∵AB=2cm，BC=2AB，
∴BC=4cm，
∴AC=AB+BC=6cm，
∵D为AC中点，
∴AD=
AC=3cm，∴BD=AD-AB=3cm-2cm=1cm，
故答案为：BC，6，AC，3，AB，1．
点评：本题考查了线段中点和求两点间的距离的应用，关键是求出AC、AD长和得出BD=AD-AB．
练习册系列答案
相关题目
11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形ABCD的边长为4，FG=3，FP=1，则△DEK的面积为
8、正方形ABCD，正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，且G为BC的三等分点，R为EF中点，正方形BEFG的边长为4，则△DEK的面积为（ ）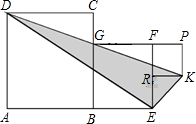
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，已知正方形BEFG的边长为3，则△DEK的面积为
已知：如图所示，点C在线段AB上，分别以AC、BC为一边作为等边△ACM和等边△BCN，连接AN、BM．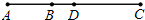
如图所示，点C在线段AB的延长线上，且BC=2AB，D是AC的中点，若AB=2cm，求BD的长．