Question

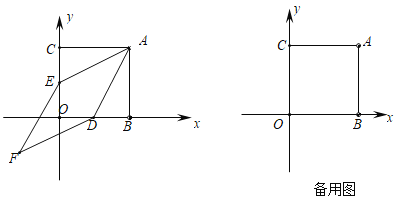
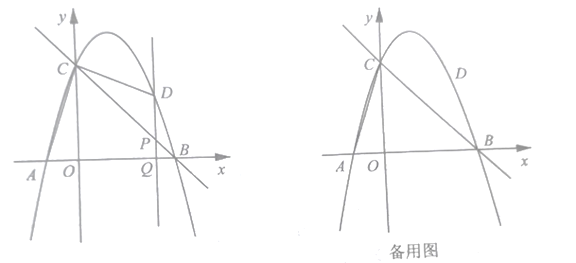
【题目】如图，在平面直角坐标系中，直线交坐标轴于两点，抛物线经过两点，且交轴于另一点.点为第一象限内抛物线上一动点，过点作交于点，交轴于点．

（1）求抛物线的解析式；

（2）设点的横坐标为在点移动的过程中，存在求出此时的值；

（3）在抛物线上取点在坐标系内取点问是否存在以为顶点且以为边的矩形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在，点的坐标为或．

【解析】

（1）先利用一次函数与坐标轴相交，求出B、C两点的坐标，再根据抛物线解析式及A、B两点坐标设出交点式，再将C的坐标代入求出a的值即可得到抛物线解析式；

（2）如图，过点D作DM⊥BC于M，点P（m，m＋3），点D（m，m2＋2m＋3），利用参数求出DM，CM的长，由锐角三角函数可求解；
（3）分两种情况讨论，当CE⊥BC时或BE⊥BC时，分别求出直线CE的方程或BE的方程，联立方程组可求解．

直线交坐标轴于两点，

点的坐标为，点的坐标为

点的坐标为，点的坐标为

设抛物线的解析式为．

将代入．

得

抛物线解析式为．

过点作于点，如图1所示

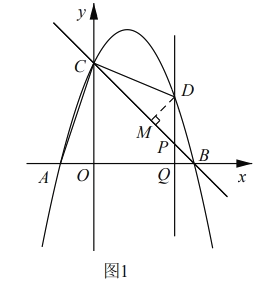
设点坐标为，则点坐标为

．

在中，

在中，

在中，，

在中，．

在中，

，

在中，由勾股定理，

得

又

解得(舍去)，

的值为

（3）存在，
若CE⊥BC时，
∴直线CE解析式为：y＝x＋3，
∴
∴(舍去)或者
∴点E坐标（1，4），
若BE⊥BC时，
∴直线BE解析式为：y＝x3，
∴
∴（舍去），或者
∴点E坐标（2，5），
综上所述：当点E（1，4）或（2，5）时，以C、B、E、F为顶点且以CB为边的矩形．