题目内容
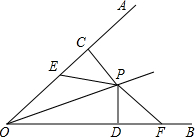 如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.
如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.考点:全等三角形的判定与性质,角平分线的性质
专题:几何图形问题
分析:∠AOP=∠BOP,利用“HL”证明Rt△PCE≌Rt△PDF,由全等三角形的性质可知:PC=PD,所以C在∠AOB的平分线上,问题得证.
解答:解:∠AOP=∠BOP,
理由如下:
∵PC⊥OA于C,PD⊥OB于D,
∴∠PCE=∠PDF=90°,
在Rt△PCE和Rt△PDF中,
,
∴Rt△PCE≌Rt△PDF(HL),
∴PC=PD,
∴C在∠AOB的平分线上,
∴∠AOP=∠BOP.
理由如下:
∵PC⊥OA于C,PD⊥OB于D,
∴∠PCE=∠PDF=90°,
在Rt△PCE和Rt△PDF中,
|
∴Rt△PCE≌Rt△PDF(HL),
∴PC=PD,
∴C在∠AOB的平分线上,
∴∠AOP=∠BOP.
点评:本题考查了全等三角形的判定和性质以及角平分线的性质定理的逆定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
一个圆心角为120°的扇形的弧长为4π,则该扇形的面积为( )
| A、6π | B、12π |
| C、18π | D、24π |
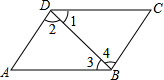 如图,下面推理正确的是( )
如图,下面推理正确的是( )| A、∵∠1=∠3,∴AD∥BC |
| B、∵∠A+∠1+∠2=180°,∴AD∥BC |
| C、∵∠A+∠3+∠4=180°,∴AB∥CD |
| D、∵∠2=∠4,∴AD∥BC |
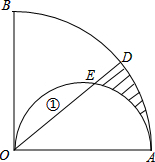 如图,∠BOA=90°,∠AOD=45°,以AO为直径画半圆交OD于E,如果图中①的面积为1cm2,求阴影部分的面积.
如图,∠BOA=90°,∠AOD=45°,以AO为直径画半圆交OD于E,如果图中①的面积为1cm2,求阴影部分的面积.