题目内容
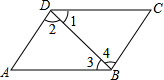 如图,下面推理正确的是( )
如图,下面推理正确的是( )| A、∵∠1=∠3,∴AD∥BC |
| B、∵∠A+∠1+∠2=180°,∴AD∥BC |
| C、∵∠A+∠3+∠4=180°,∴AB∥CD |
| D、∵∠2=∠4,∴AD∥BC |
考点:平行线的判定
专题:
分析:根据平行线的判定定理分别对每一项进行分析即可.
解答:解:A、∵∠1=∠3,∴AB∥CD,故本选项错误;
B、∵∠A+∠1+∠2=180°,∴AB∥CD,故本选项错误;
C、∵∠A+∠3+∠4=180°,∴AD∥BC,故本选项错误;
D、∵∠2=∠4,∴AD∥BC,故本选项正确;
故选D.
B、∵∠A+∠1+∠2=180°,∴AB∥CD,故本选项错误;
C、∵∠A+∠3+∠4=180°,∴AD∥BC,故本选项错误;
D、∵∠2=∠4,∴AD∥BC,故本选项正确;
故选D.
点评:此题考查了平行线的判定,平行线的判定定理是:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
若x+2和3x-14是某一个数的平方根,则这个数是( )
| A、25 | B、8 | C、5 | D、3 |
圆内接正六边形边长为6,则该圆的内接正三角形边长为( )
A、6
| ||
B、9
| ||
C、6
| ||
| D、12 |
在四边形ABCD中,若有下列四个条件:
①AB∥CD;②AD=BC;③∠A=∠C;④AB=CD.
现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )
①AB∥CD;②AD=BC;③∠A=∠C;④AB=CD.
现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )
| A、3组 | B、4组 | C、5组 | D、6组 |
如图,在图1第一个天平上,砝码A的质量等于砝码B加上砝码C的质量,在图2第二个天平上,砝码A加上砝码B的质量等于3个砝码C的质量.请你判断:1个砝码A与几个砝码C的质量相等( )

| A、2 | B、3 | C、4 | D、5 |
下列各组中不能构成三角形的一组是( )
| A、5,12,13 |
| B、4,7,7 |
| C、101,102,103 |
| D、2a,3a,5a(a>0) |
把抛物线y=2x2向右平移m个单位经过点(3,2),则m的值为( )
| A、3 | B、2 | C、4 | D、4或2 |
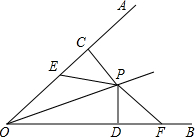 如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.
如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.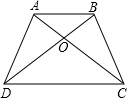 如图,四边形ABCD中,对角形AC、BD相交于点O.证明:AB+BC+CD+AD>AC+BD.
如图,四边形ABCD中,对角形AC、BD相交于点O.证明:AB+BC+CD+AD>AC+BD.