题目内容
若解关于x的方程
+2=
产生增根,求k的值.
| k |
| x-3 |
| 4-x |
| x-3 |
考点:分式方程的增根
专题:计算题
分析:增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x-3=0,得到x=3,然后代入化为整式方程的方程算出k的值.
解答:解:方程两边都乘(x-3),得
k+2(x-3)=4-x,
∵方程有增根,
∴最简公分母x-3=0,即增根是x=3,
把x=3代入整式方程,得k=1.
k+2(x-3)=4-x,
∵方程有增根,
∴最简公分母x-3=0,即增根是x=3,
把x=3代入整式方程,得k=1.
点评:本题考查了分式方程的增根,解决增根问题的步骤:
①确定增根的值;
②化分式方程为整式方程;
③把增根代入整式方程即可求得相关字母的值.
①确定增根的值;
②化分式方程为整式方程;
③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
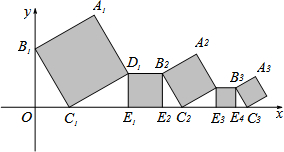 已知,在平面直角坐标系中放置了5个如图的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,且B1C1∥B2C2∥B3C3,则点B3的坐标是( )
已知,在平面直角坐标系中放置了5个如图的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,且B1C1∥B2C2∥B3C3,则点B3的坐标是( )A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(3+
|
下列各组中不能构成三角形的一组是( )
| A、5,12,13 |
| B、4,7,7 |
| C、101,102,103 |
| D、2a,3a,5a(a>0) |
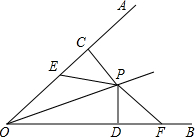 如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.
如图,已知P是∠AOB内一点且PC⊥OA于C,PD⊥OB于D且EC=FD,EP=PF,猜想∠AOP和∠BOP的大小关系并说明你的理由.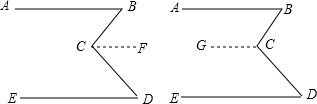 如图,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.
如图,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.