题目内容
如图,在△ABC中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).
(1)在运动过程中,△DEF能否为以DE为腰的等腰三角形?若能,请求出t的值;若不能, 试说明理由.
(2)以E为圆心,EF长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙E与边AC有1个公共点?
(3)设M、N分别是DF、EF的中点,请直接写出在整个运动过程中,线段MN所扫过的图形的面积.
(1)在运动过程中,△DEF能否为以DE为腰的等腰三角形?若能,请求出t的值;若不能, 试说明理由.
(2)以E为圆心,EF长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙E与边AC有1个公共点?
(3)设M、N分别是DF、EF的中点,请直接写出在整个运动过程中,线段MN所扫过的图形的面积.

(1)t=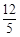 或
或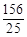 ;(2)
;(2)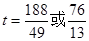 <
<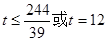 ;(3)
;(3)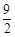 cm2
cm2
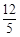 或
或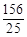 ;(2)
;(2)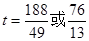 <
<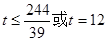 ;(3)
;(3)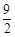 cm2
cm2试题分析:(1)分
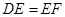 与
与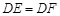 两种情况结合相似三角形的性质分析即可;
两种情况结合相似三角形的性质分析即可;(2)根据切线的性质分⊙E与边AC相切、EF=EA、EF=EC这三中情况分析即可;
(3)根据线段MN运动的特征结合相应的面积公式即可求得结果.
(1)
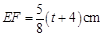
分两种情况讨论:
当
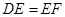 时,
时,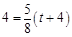 ,解得:
,解得: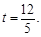
当
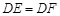 时,有
时,有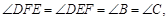
∴△DEF∽△ABC
∴
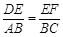 ,即
,即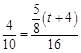 ,解得:
,解得: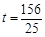 .
. 综上所述,当t=
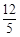 或
或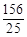 秒时,△
秒时,△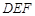 为等腰三角形;
为等腰三角形;(2)⊙E与边AC相切时,t=
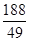
EF=EA时,
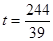
EF=EC时,
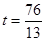
所以当
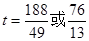 <
<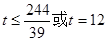 时,⊙E与边AC有1个公共点;
时,⊙E与边AC有1个公共点;(3)整个运动过程中,MN所扫过的图形的面积为
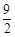 cm2.
cm2.点评:圆的综合题是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则弦CD的长为( )
,则弦CD的长为( )




 ,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2-
,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2- )
)
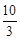 cm时,量得锯痕AB=
cm时,量得锯痕AB=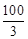 cm,问圆木的直径是多少cm?
cm,问圆木的直径是多少cm?





 与
与 外切,
外切,