题目内容
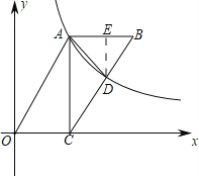
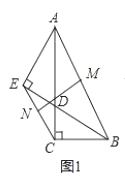
【题目】如图1，在
中，
，
，点
在边
上，连接
，过
作的垂线交的延长线于点
．
（1）若
，
分别为线段
，
的中点，如图1，求证：
；
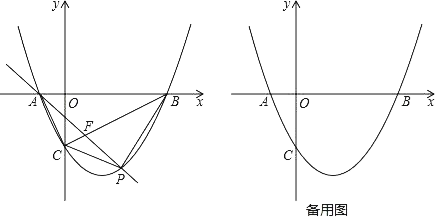
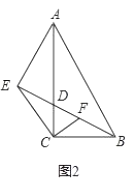
（2）如图2，过点
作
交于点
，求证：
；
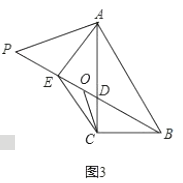
（3）如图3，以
为一边作一个角等于
，这个角的另一边与
的延长线交于
点，
为
的中点，连接
，求证：
．
【答案】（1）详见解析；（2）详见解析；（3）详见解析
【解析】
（1）连接EM、CM，直角三角形斜边上的中线等于斜边的一半得EM=CM；再由等腰三角形三线合一的性质得
出结论；
（2）证明△AEC∽△BFC，得
，由AC=2BC得AE=2BF；
（3）证明△ACB∽△AEP，得
，从而知道AE=2PE，由AE=2BF得PE=BF；根据直角三角形斜边中线等于斜边一半得OC=
EF，代入得结论．
解：证明：（1）如图1，连接
、
，
，
是
的中点，
，
，
，
是
的中点，
；
（2）如图2，
，
，
，
，
，
，
，
，
，
，
，
；
（3）如图，过点
作
交
于点
，
，
，
，
，
，
，
，
，
为
的中点，
，
，
．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
