题目内容
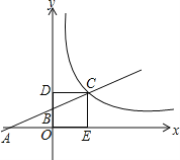
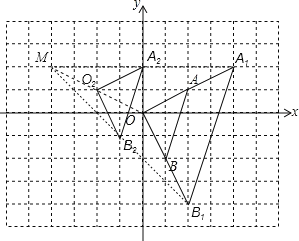
【题目】如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的相似比为2:1,并写出点A的对应点A1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2,并写出点A2的坐标;
(3)判断△OA1B1与△O2A2B2,能否是关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.
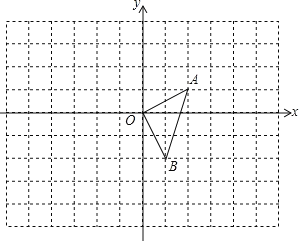
【答案】(1)见解析,A1(4,2);(2)见解析,A2(0,2);(3)见解析,M(﹣4,2).
【解析】
(1)利用位似图形的性质得出对应点位置,进而得出答案;
(2)利用平移变换规律得出对应点位置,进而得出答案;
(3)连接B1B2,OO2,A1A2并延长,它们交于一点,则可判定是位似图形,交点即为位似中心,进而得出答案.
解:(1)如图所示:△OA1B1即为所求,A1(4,2);
(2)如图所示:△O2A2B2即为所求,A2(0,2);
(3)位似中心M如图所示,M(﹣4,2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.