Question

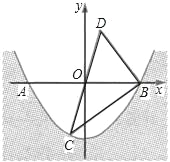
【题目】某水渠的横截面呈抛物线，水面的宽度为AB（单位：米），现以AB所在直线为x轴，以抛物线的对称轴为y轴建立如图所示的平面直角坐标系，设坐标原点为O．已知AB=8米，设抛物线解析式为y=ax2﹣4．

（1）求a的值；

（2）点C（﹣1，m）是抛物线上一点，点C关于原点O的对称点为点D，连接CD，BC，BD，求△BCD的面积．

Answer 1

【答案】(1) (2) 15

【解析】【试题分析】（1）以抛物线的对称轴为y轴，AB=8，则B（4，0），将点B代入即可.

（2）先代入二次函数表达式，求出点C的坐标C（﹣1，﹣），再求出关于原点的对称点D的坐标（1，），最后再求出两个三角形的面积和.

【试题解析】

（1）∵AB=8，由抛物线的性质可知OB=4，

∴B（4，0），

把B点坐标代入解析式得：16a﹣4=0，

解得：a=；

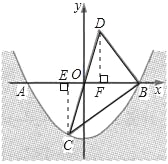
（2）过点C作CE⊥AB于E，过点D作DF⊥AB于F，

∵a=，

∴y=x2﹣4，

令x=﹣1，

∴m=×（﹣1）2﹣4=﹣，

∴C（﹣1，﹣），

∵C关于原点对称点为D，

∴D的坐标为（1，），

则CE=DF=，

S△BCD=S△BOD+S△BOC=OBDF+OBCE=×4×+×4×=15，

∴△BCD的面积为15平方米．