题目内容
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
【答案】(1) a1=![]() .(2) a2=
.(2) a2=![]() ’ (3) an=
’ (3) an=![]() .
.
【解析】分析:(1)设PQ与![]() 交于点D,连接
交于点D,连接![]() ,得出OD=
,得出OD= ![]() -O
-O![]() ,用含
,用含![]() 的代数式表示OD,在△O
的代数式表示OD,在△O![]() D中,根据勾股定理求出正三角形的边长
D中,根据勾股定理求出正三角形的边长![]() ;(2)设PQ与
;(2)设PQ与![]()
![]() 交于点E,连接
交于点E,连接![]() O,得出OE=
O,得出OE=![]() E-O
E-O![]() ,用含
,用含![]() 的代数式表示OE,在△O
的代数式表示OE,在△O![]() E中,根据勾股定理求出正三角形的边长
E中,根据勾股定理求出正三角形的边长![]() ;(3)设PQ与
;(3)设PQ与![]()
![]() 交于点F,连接
交于点F,连接![]() O,得出OF=
O,得出OF=![]() F-O
F-O![]() ,用含an的代数式表示OF,在△O
,用含an的代数式表示OF,在△O![]() F中,根据勾股定理求出正三角形的边长an.
F中,根据勾股定理求出正三角形的边长an.
本题解析:
(1)易知△A1B1C1的高为![]() ,则边长为
,则边长为![]() ,
,
∴a1=![]() .
.
(2)设△A1B1C1的高为h,则A2O=1-h,连结B2O,设B2C2与PQ交于点F,则有OF=2h-1.
∵B2O2=OF2+B2F2,∴1=(2h-1)2+![]() .
.
∵h=![]() a2,∴1=(
a2,∴1=(![]() a2-1)2+
a2-1)2+![]() a22,
a22,
解得a2=![]() .
.
(3)同(2),连结BnO,设BnCn与PQ交于点F,则有BnO2=OF2+BnF2,
即1=(nh-1)2+![]() .
.
∵h=![]() an,∴1=
an,∴1=![]() an2+
an2+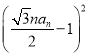 ,
,
解得an=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目