题目内容
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
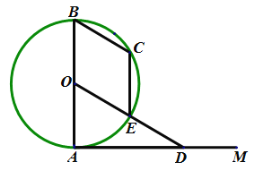
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;
(2)依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.
解:如图,连接OC,∵AM⊥AB,
∴∠OAD=90°.
∵OA=OC,OD=OD,AD=DC,
∴△OAD≌△OCD,
∴∠OCD=∠OAD=90°.
∴OC⊥CD,
∴CD是⊙O的切线.
(2)∵四边形OECB是菱形,
∴OE=CE.
又∵OC=OE,
∴OC=OE=CE.
∴∠CEO=60°.
∵CE∥AB,
∴∠AOD=60°.
在Rt△OAD中,∠AOD=60°,AO=![]() 1,
1,
∴AD=![]() .
.
故答案为:![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目