题目内容
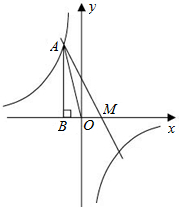 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
| k |
| x |
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长.
分析:(1)根据点A的横坐标与△AOB的面积求出AB的长度,从而得到点A的坐标,然后利用待定系数法求出反比例函数解析式,再利用反比例函数解析式求出点C的坐标,根据点A与点C的坐标利用待定系数法即可求出直线y=ax+b的解析式;
(2)根据直线y=ax+b的解析式,取y=0,求出对应的x的值,得到点M的坐标,然后求出BM的长度,在△ABM中利用勾股定理即可求出AM的长度.
(2)根据直线y=ax+b的解析式,取y=0,求出对应的x的值,得到点M的坐标,然后求出BM的长度,在△ABM中利用勾股定理即可求出AM的长度.
解答:解:(1)∵点A(-1,m)在第二象限内,
∴AB=m,OB=1,
∴S△ABO=
AB•BO=2,
即:
×m×1=2,
解得m=4,
∴A (-1,4),
∵点A (-1,4),在反比例函数y=
的图象上,
∴4=
,
解得k=-4,
∴反比例函数为y=-
,
又∵反比例函数y=-
的图象经过C(n,-2)
∴-2=
,
解得n=2,
∴C (2,-2),
∵直线y=ax+b过点A (-1,4),C (2,-2)
∴
,
解方程组得
,
∴直线y=ax+b的解析式为y=-2x+2;
(2)当y=0时,即-2x+2=0,
解得x=1,
∴点M的坐标是M(1,0),
在Rt△ABM中,
∵AB=4,BM=BO+OM=1+1=2,
由勾股定理得AM=
=
=2
.
∴AB=m,OB=1,
∴S△ABO=
| 1 |
| 2 |
即:
| 1 |
| 2 |
解得m=4,
∴A (-1,4),
∵点A (-1,4),在反比例函数y=
| k |
| x |
∴4=
| k |
| -1 |
解得k=-4,
∴反比例函数为y=-
| 4 |
| x |
又∵反比例函数y=-
| 4 |
| x |
∴-2=
| -4 |
| n |
解得n=2,
∴C (2,-2),
∵直线y=ax+b过点A (-1,4),C (2,-2)
∴
|
解方程组得
|
∴直线y=ax+b的解析式为y=-2x+2;
(2)当y=0时,即-2x+2=0,
解得x=1,
∴点M的坐标是M(1,0),
在Rt△ABM中,
∵AB=4,BM=BO+OM=1+1=2,
由勾股定理得AM=
| AB2+BM2 |
| 42+22 |
| 5 |
点评:本题主要考查了反比例函数,待定系数法求函数解析式,勾股定理,综合性较强,但只要细心分析题目难度不大.

练习册系列答案
相关题目
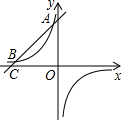 如图,已知反比例函数
如图,已知反比例函数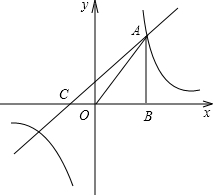 如图,已知反比例函数
如图,已知反比例函数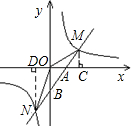 如图,已知反比例函数y=
如图,已知反比例函数y=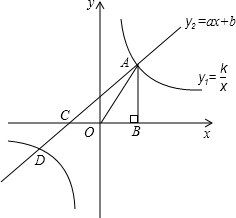 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=