题目内容
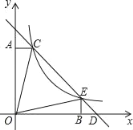
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+b分别交x,y轴于点A、C,抛物线y=ax2+x+4经过A、C两点,交x轴于另外一点B.
(1)求抛物线的解析式;
(2)点P在第一象限内抛物线上,连接PB、PC,作平行四边形PBDC,DE⊥y轴于点E,设点P 的横坐标为t,线段DE的长度为d,求d与t之间的函数关系式.
(3)在(2)的条件下,延长BD交直线AC与点F,连接OF,若∠AFO=∠BFO,求点P的坐标.
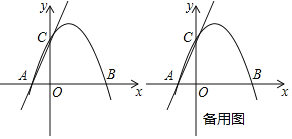
【答案】(1)y=-![]() x2+x+4.(2)d =4-t(0<t<4).(3)点P坐标为(
x2+x+4.(2)d =4-t(0<t<4).(3)点P坐标为(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法即可解决问题.
(2)如图1中,设P(t,-![]() x2+x+4),D(x,y).根据平行四边形的性质对角线互相平分,利用中点坐标公式,列出方程即可解决问题.
x2+x+4),D(x,y).根据平行四边形的性质对角线互相平分,利用中点坐标公式,列出方程即可解决问题.
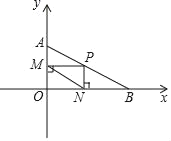
(3)如图2中,作OM⊥AC于M,ON⊥BF于N,NE⊥OB于E.先求出点N的坐标,求出直线NB的解析式,再求出直线PC的解析式,解方程组即可解决问题.
(1)对于抛物线y=ax2+x+4,令x=0,得y=4,
∴C(0,4),把C(0,4),代入y=2x+b中,得b=4,
∴直线解析式为y=2x+4,令Y=0,得x=-2,
∴A(-2,0),把A(-2,0)代入y=ax2+x+4,得a=-![]() ,
,
∴抛物线的解析式为y=-![]() x2+x+4.
x2+x+4.
(2)如图1中,设P(t,-![]() x2+x+4),D(x,y).
x2+x+4),D(x,y).

∵C(0,4),B(4,0),四边形CPBD是平行四边形,
∴![]() ,x=4-t,
,x=4-t,
∴d=DE=x=4-t(0<t<4).
(3)如图2中,作OM⊥AC于M,ON⊥BF于N,NE⊥OB于E.
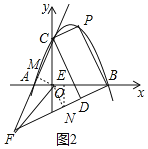
∵∠OFA=∠OFB,OM⊥FC,ON⊥FB,
∴OM=ON,
∵![]() OAOC=
OAOC=![]() ACOM,OA=2,OC=4,AC=
ACOM,OA=2,OC=4,AC=![]() ,
,
∴ON=OM=![]() ,
,
∵BN=![]() ,
,
∵![]() ONBN=
ONBN=![]() OBEN,
OBEN,
∴EN=![]() ,OE=
,OE=![]() ,
,
∴N(![]() ,-
,-![]() ),
),
设直线BN的解析式为y=kx+b,则有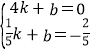 ,解得
,解得  ,
,
∵PC∥BN,
∴直线PC的解析式为y=![]() x+4,
x+4,
由 ,解得
,解得![]() 或
或 ,
,
∴点P坐标为(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.