题目内容
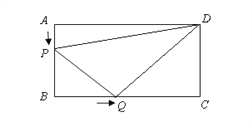
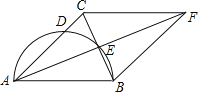
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=6,BE=2![]() ,求四边形ABFC的面积.
,求四边形ABFC的面积.
【答案】(1)证明见解析;(2)16![]() .
.
【解析】
(1)根据圆周角定理得到∠AEB=90°,根据线段垂直平分线的性质、菱形的判定定理证明结论;
(2)根据菱形的性质求出CE,根据切割线定理求出CD,根据勾股定理、菱形的面积公式计算,得到答案.
(1)证明:∵AB是圆的直径,
∴∠AEB=90°,
∵EF=AE,
∴CB是线段AF的垂直平分线,
∴BA=BF,CA=CF,
∵AB=AC,
∴BA=BF=CA=CF,
∴四边形ABFC是菱形;
(2)解:∵四边形ABFC是菱形,
∴CE=BE=2![]() ,
,
由切割线定理得,CDCA=CECB,即CD(CD+6)=2![]() ×4
×4![]() ,
,
解得,CD1=2,CD2=-8(舍去)
∴AC=8,
由勾股定理得,AE=![]() =2
=2![]() ,
,
∴AF=4![]() ,
,
则四边形ABFC的面积=![]() ×4
×4![]() ×4
×4![]() =16
=16![]() .
.

练习册系列答案
相关题目