Question

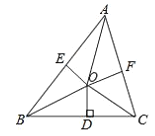
【题目】已知：如图 ，AD 是∠BAC 的平分线，且 DF⊥AC 于 F，∠B=90°，DE=DC.

（1）求证：BE=CF.

（2）若△ADE 和△DCF 的面积分别是12和5，求△ABC 的面积.

（3）请你写出∠BAC与∠CDE有什么数量关系？并说明理由.

Answer 1

【答案】（1）详见解析；（2）39；（3）互补；

【解析】

（1）先由角平分线的性质就可以得出DB=DF，再证明△BDE≌△FDC就可以求出结论．（2）由△BDE和△FDC面积相等，△ABD和△ADF面积相等，转换得出△ABC的面积即可；(3)通过∠ACD=∠BED推出∠ACD+∠ AED=180°，再通过四边形AEDC的内角和为360°即可求出∠BAC与∠CDE的关系.

（1）证明：

∵∠B=90°，

∴BD⊥AB．

∵AD为∠BAC的平分线，且DF⊥AC，

∴DB=DF．

在Rt△BDE和Rt△FDC中，

∴Rt△BDE≌Rt△FDC（HL），

∴BE=CF

（2）解：∵△BDE≌△FDC

∴△ BDE的面积为5，

则S△ABD=17，

∵AD平分∠BAC，DB⊥AB，DF⊥AC，

∴S△ABD=S△ADF=17，

∴S△ABC=17+17+5=39

（3）解：∵△BDE≌△FDC

∴∠ACD=∠BED，

∵∠ BED+∠AED=180°，

∴∠ACD+∠AED=180°，

在四边形AEDC中，

∵四边形内角和为360°，∠ACD+∠AED=180°，

∴∠BAC +∠CDE=180°，即∠BAC 与∠CDE互补.