题目内容
【题目】如图,已知△ABC的周长是21,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
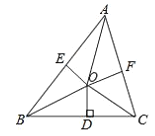
(1)试判断线段OD、OE、OF的大小关系.
(2)求△ABC的面积.
【答案】(1)OD=OE=OF,理由见解析;(2)31.5.
【解析】
(1)根据角平分线上的点到角两边的距离相等即可得出OD、OE、OF的大小关系;
(2)由S△ABC=S△BOC+ S△AOB+ S△AOC,利用三角形的面积公式进行求解即可.
解:(1)OD=OE=OF,理由如下:
∵BO平分∠ABC,OD⊥BC,OE⊥AB,
∴OD=OE,
∵CO平分∠ACB,OD⊥BC,OF⊥AC,
∴OD=OF,
∴OD=OE=OF;
(2)∵S△ABC=S△BOC+ S△AOB+ S△AOC,
S△BOC=![]() ,S△AOB=
,S△AOB=![]() , S△AOC=
, S△AOC=![]() ,
,
∴S△ABC=![]() +
+![]() +
+![]() ,
,
∵OD=OE=OF,
∴S△ABC=![]() (BC+AB+AC),
(BC+AB+AC),
∵AB+BC+AC=21,OD=3,
∴S△ABC=![]() =31.5.
=31.5.

练习册系列答案
相关题目