题目内容
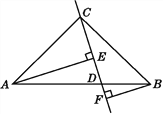
【题目】如图:在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.
【答案】AC⊥BC,理由见解析.
【解析】试题分析:根据AE⊥CD,BF⊥CD,得到∠AEC=∠BFC=90°,由于CF=EE+CF,CE=BF,得到CF=EF+BF,于是得到AE=CF,证得Rt△ACE≌Rt△CBF,得出∠BCF=∠CAE,然后根据∠ACB=∠BCF+∠ACE=∠CAE+∠AEC=90°,即可得到结论.
试题解析:AC⊥BC.
理由如下:∵AE⊥CD,BF⊥CD,
∴∠AEC=∠BFC=90°,
∴∠CAE+∠ACE=90°,
∵CF=EE+CF,CE=BF,
∴CF=EF+BF,
∵AE=EF+BF,
∴AE=CF,
在Rt△ACE≌Rt△CBF中,

∴Rt△ACE≌Rt△CBF,
∴∠BCF=∠CAE,
∴∠ACB=∠BCF+∠ACE=∠CAE+∠AEC=90°,
∴AC⊥BC.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目