题目内容
【题目】定义:我们把对角线互相垂直的四边形叫做垂美四边形.
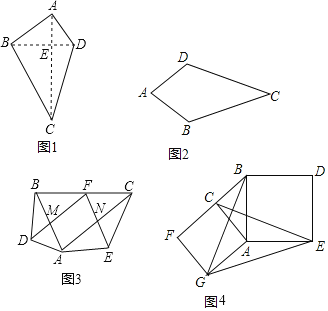
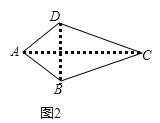
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:
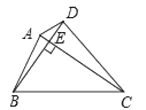
①如图1,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
②如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在![]() 外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
(3)问题解决:
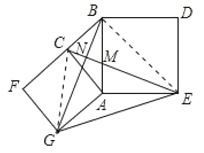
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG,GE,已知AC=2,AB=5.求GE的长度.
【答案】(1)四边形ABCD是垂美四边形,证明见解析 (2)①![]() ,证明见解析;②四边形FMAN是矩形,证明见解析 (3)
,证明见解析;②四边形FMAN是矩形,证明见解析 (3)![]()
【解析】
(1)根据垂直平分线的判定定理证明即可;
(2)①根据垂直的定义和勾股定理解答即可;②根据在Rt△ABC中,点F为斜边BC的中点,可得![]() ,再根据△ABD和△ACE是等腰三角形,可得
,再根据△ABD和△ACE是等腰三角形,可得![]() ,再由(1)可得,
,再由(1)可得,![]() ,从而判定四边形FMAN是矩形;
,从而判定四边形FMAN是矩形;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
(1)四边形ABCD是垂美四边形
连接AC、BD
∵![]()
∴点A在线段BD的垂直平分线上
∵![]()
∴点C在线段BD的垂直平分线上
∴直线AC是线段BD的垂直平分线
∴![]()
∴四边形ABCD是垂美四边形;
(2)①![]() ,理由如下
,理由如下
如图,已知四边形ABCD中,![]() ,垂足为E
,垂足为E
![]()
![]()
由勾股定理得
![]()
![]()
![]()
②四边形FMAN是矩形,理由如下
如图,连接AF

∵在Rt△ABC中,点F为斜边BC的中点
![]()
∵△ABD和△ACE是等腰三角形
![]()
由(1)可得,![]()
∵![]()
![]()
∴四边形FMAN是矩形;
(3)连接CG、BE,
![]()
![]() ,即
,即![]()
在△AGB和△ACE中
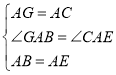
![]()
![]()
∵![]()
![]() ,即
,即![]()
∴四边形CGEB是垂美四边形
由(2)得![]()
![]()
![]()
![]()
![]() .
.

【题目】在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm, 整点P从原点0出发,速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s) | 可以得到整点P的坐标 | 可以得到整点P的个数 |
1 | (0,1)(1,0) | 2 |
2 | (0,2)(1,1)(2,0) | 3 |
3 | (0,3)(1,2)(2,1)(3,0) | 4 |
. | · | . |
根据上表中的规律,回答下列问题:
(1)当整点P从点0出发4s时,可以得到的整点的个数为______个.
(2)当整点P从点O出发8s时,在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
(3)当整点P从点0出发______s时,可以得到整点(16,4)的位置.