Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ“—÷™![]() «Ļō”ŕ
«Ļō”ŕ![]() Ķń∂Ģīő∂ŗŌÓ Ĺ£¨«“∂ĢīőŌÓŌĶ żļÕ“ĽīőŌÓŌĶ ż∑÷Īūő™
Ķń∂Ģīő∂ŗŌÓ Ĺ£¨«“∂ĢīőŌÓŌĶ żļÕ“ĽīőŌÓŌĶ ż∑÷Īūő™![]() ļÕ
ļÕ![]() £¨‘ŕ ż÷Š…Ō
£¨‘ŕ ż÷Š…Ō![]() °Ę
°Ę![]() °Ę
°Ę![]() »żĶ„ňý∂‘”¶Ķń ż∑÷Īū «
»żĶ„ňý∂‘”¶Ķń ż∑÷Īū «![]() °Ę
°Ę![]() °Ę
°Ę![]() .
.
![]()
£®1£©”–“Ľ∂ĮĶ„![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑Ę£¨“‘√Ņ√Ž
≥Ų∑Ę£¨“‘√Ņ√Ž![]() łŲĶ•őĽĶńňŔ∂»ŌÚ◊ů‘ň∂Į£¨∂ŗ…Ŕ√Žļů£¨
łŲĶ•őĽĶńňŔ∂»ŌÚ◊ů‘ň∂Į£¨∂ŗ…Ŕ√Žļů£¨![]() ĶĹ
ĶĹ![]() °Ę
°Ę![]() °Ę
°Ę![]() ĶńĺŗņŽļÕő™
ĶńĺŗņŽļÕő™![]() łŲĶ•őĽ£Ņ
łŲĶ•őĽ£Ņ
£®2£©‘ŕ£®1£©ĶńŐűľĢŌ¬£¨ĶĪĶ„![]() “∆∂ĮĶĹĶ„
“∆∂ĮĶĹĶ„![]() ĪŃĘľīĶŰÕ∑£¨ňŔ∂»≤ĽĪš£¨Õ¨ ĪĶ„
ĪŃĘľīĶŰÕ∑£¨ňŔ∂»≤ĽĪš£¨Õ¨ ĪĶ„![]() ļÕĶ„
ļÕĶ„![]() ∑÷Īūī”Ķ„
∑÷Īūī”Ķ„![]() ļÕĶ„
ļÕĶ„![]() ≥Ų∑Ę£¨ŌÚ”“‘ň∂Į£¨Ķ„
≥Ų∑Ę£¨ŌÚ”“‘ň∂Į£¨Ķ„![]() ĶńňŔ∂»
ĶńňŔ∂»![]() łŲĶ•őĽ
łŲĶ•őĽ![]() √Ž£¨Ķ„
√Ž£¨Ķ„![]() ĶńňŔ∂»
ĶńňŔ∂»![]() łŲĶ•őĽ
łŲĶ•őĽ![]() √Ž.…ŤĶ„
√Ž.…ŤĶ„![]() °Ę
°Ę![]() °Ę
°Ę![]() ňý∂‘”¶Ķń ż∑÷Īū «
ňý∂‘”¶Ķń ż∑÷Īū «![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨Ķ„
£¨Ķ„![]() ≥Ų∑ĘĶń Īľšő™
≥Ų∑ĘĶń Īľšő™![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨«ů
Ī£¨«ů![]() Ķń÷Ķ.
Ķń÷Ķ.
°ĺīūįł°Ņ£®1£©2√Ž£Ľ£®2£©8t-26
°ĺĹ‚őŲ°Ņ
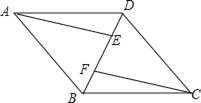
£®1£©Ō»łýĺ›Ő‚“‚«ů≥Ųa°Ęb°ĘcĶń÷Ķ£¨‘Ŕłýĺ›Õľ–őĶ√ĶĹ£ļ![]() ĶĹ
ĶĹ![]() °Ę
°Ę![]() °Ę
°Ę![]() ĶńĺŗņŽļÕő™
ĶńĺŗņŽļÕő™![]() łŲĶ•őĽ£¨‘Úīň ĪP“Ľ∂®‘ŕBļÕ‘≠Ķ„÷ģľš£¨…ŤĶ„PĪŪ ĺĶń żő™x£¨Ń–≥Ų∑Ĺ≥Ő£¨Ĺ‚∑Ĺ≥Ő£¨ī”∂Ý«ůĶ√ Īľš£Ľ
łŲĶ•őĽ£¨‘Úīň ĪP“Ľ∂®‘ŕBļÕ‘≠Ķ„÷ģľš£¨…ŤĶ„PĪŪ ĺĶń żő™x£¨Ń–≥Ų∑Ĺ≥Ő£¨Ĺ‚∑Ĺ≥Ő£¨ī”∂Ý«ůĶ√ Īľš£Ľ
£®2£©Ō»«ů≥ŲĶ„P◊∑…ŌĶ„MĶń Īľšő™![]() √Ž£¨Ķ„N◊∑…ŌĶ„MĶń Īľšő™
√Ž£¨Ķ„N◊∑…ŌĶ„MĶń Īľšő™![]() £¨Ķ„N◊∑…ŌĶ„PĶń Īľšő™
£¨Ķ„N◊∑…ŌĶ„PĶń Īľšő™![]() £¨”…īňĽ≠≥Ų∂‘”¶ĶńÕľ–ő£¨‘ŔņŻ”√ĺÝ∂‘÷ĶĶń–‘÷ «ůĹ‚.
£¨”…īňĽ≠≥Ų∂‘”¶ĶńÕľ–ő£¨‘ŔņŻ”√ĺÝ∂‘÷ĶĶń–‘÷ «ůĹ‚.
£®1£©“Úő™![]() «Ļō”ŕ
«Ļō”ŕ![]() Ķń∂Ģīő∂ŗŌÓ Ĺ£¨«“∂ĢīőŌÓŌĶ żļÕ“ĽīőŌÓŌĶ ż∑÷Īūő™
Ķń∂Ģīő∂ŗŌÓ Ĺ£¨«“∂ĢīőŌÓŌĶ żļÕ“ĽīőŌÓŌĶ ż∑÷Īūő™![]() ļÕ
ļÕ![]() £¨
£¨
ňý“‘a=10,b=6,c=-3,
ĶĪĶ„P‘ŕA°ĘBŃĹĶ„÷ģľš Ī£¨≤ĽŅ…ń‹īś‘ŕĶ„![]() ĶĹ
ĶĹ![]() °Ę
°Ę![]() °Ę
°Ę![]() ĶńĺŗņŽļÕő™
ĶńĺŗņŽļÕő™![]() łŲĶ•őĽ£Ľ
łŲĶ•őĽ£Ľ
ĶĪĶ„P‘ŕĶ„CļÕ‘≠Ķ„÷ģľš Ī£¨≤ĽŅ…ń‹īś‘ŕĶ„![]() ĶĹ
ĶĹ![]() °Ę
°Ę![]() °Ę
°Ę![]() ĶńĺŗņŽļÕő™
ĶńĺŗņŽļÕő™![]() łŲĶ•őĽ£Ľ
łŲĶ•őĽ£Ľ
ĶĪĶ„P‘ŕĶ„BļÕ‘≠Ķ„÷ģľš Ī£¨…ŤPĶ„ĪŪ ĺĶń żő™x£¨‘Ú£ļ
x+3+(6-x)+(10-x)=15
Ĺ‚Ķ√x=4,
ňý“‘AP=10-4=6,
ňý“‘Ķ„P‘ň∂ĮĶń Īľšő™![]() √Ž£Ľ
√Ž£Ľ
£®2£©“Úő™Ķ„P◊∑…ŌĶ„MĶń Īľšő™![]() √Ž£¨Ķ„N◊∑…ŌĶ„MĶń Īľšő™
√Ž£¨Ķ„N◊∑…ŌĶ„MĶń Īľšő™![]() £¨Ķ„N◊∑…ŌĶ„PĶń Īľšő™
£¨Ķ„N◊∑…ŌĶ„PĶń Īľšő™![]() £¨«“
£¨«“![]() £¨
£¨
ňý“‘īň ĪĶ„∂‘”¶ĶńM°ĘN°ĘPĶńőĽ÷√»ÁÕľňý ĺ,∂‘”¶Ķń żő™![]() =3t+6°Ę
=3t+6°Ę![]() =t+10°Ę
=t+10°Ę![]() =5t-3
=5t-3
![]()
°ŗ![]()
=3t+6-(t+10)+(5t-3)-(t+10)-[(3t+6)-(5t-3)]
=3t+6-t-10+5t-3-t-10-3t-6+5t-3
=8t-26.

 łųĶō∆ŕń©łīŌįŐō—ĶĺŪŌĶŃ–īūįł
łųĶō∆ŕń©łīŌįŐō—ĶĺŪŌĶŃ–īūįł –°≤© Ņ∆ŕń©ī≥Ļō100∑÷ŌĶŃ–īūįł
–°≤© Ņ∆ŕń©ī≥Ļō100∑÷ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ ż—ß–ň»§–°◊ť—–ĺŅń≥–ÕļŇņšĻŮő¬∂»ĶńĪšĽĮ«ťŅŲ£¨∑ĘŌ÷ł√ņšĻŮĶńĻ§◊ųĻż≥Ő «£ļ
ĶĪő¬∂»īÔĶĹ…Ť∂®ő¬∂»©Ā20°ś Ī£¨÷∆ņšÕ£÷Ļ£¨īňļůņšĻŮ÷–Ķńő¬∂»Ņ™ ľ÷ūĹ•…Ō…ż£¨ĶĪ…Ō…żĶĹ©Ā4°ś Ī£¨÷∆ņšŅ™ ľ£¨ő¬∂»Ņ™ ľ÷ūĹ•Ō¬ĹĶ£¨ĶĪņšĻŮ◊‘∂Į÷∆ņš÷Ń“Ľ20°ś Ī£¨÷∆ņš‘ŔīőÕ£÷Ļ£¨£ģ£ģ
įī’’“‘…Ō∑Ĺ Ĺ—≠Ľ∑ĹÝ––
Õ¨—ß√«ľ«¬ľŃň44min ńŕ15łŲ ĪľšĶ„ņšĻŮ÷–Ķńő¬∂»y£®°ś£© ňś Īľšx£®min£© ĶńĪšĽĮ«ťŅŲ£¨÷∆≥…Ō¬ĪŪ£ļ
Īľšx/min | °≠ | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | °≠ |
ő¬∂»y/°ś | °≠ | ©Ā20 | ©Ā10 | ©Ā8°° | ©Ā5 | ©Ā4 | ©Ā8 | ©Ā12 | ©Ā16 | ©Ā20 | ©Ā10°° | ©Ā8 | ©Ā5 | ©Ā4 | °°a | ©Ā20 | °≠ |
£®1£©Õ®Ļż∑÷őŲ∑ĘŌ÷£¨ņšĻŮ÷–Ķńő¬∂»y « ĪľšxĶńļĮ ż£ģ
ĘŔĶĪ4°‹x£ľ20 Ī£¨–ī≥Ų“ĽłŲ∑ŻļŌĪŪ÷– żĺ›ĶńļĮ żĹ‚őŲ Ĺ°° °°£Ľ
ĘŕĶĪ20°‹x£ľ24 Ī£¨–ī≥Ų“ĽłŲ∑ŻļŌĪŪ÷– żĺ›ĶńļĮ żĹ‚őŲ Ĺ°° °°£Ľ
£®2£©ő¬∂»≤ĽĶÕ”ŕ©Ā8°śĶń≥÷–Ý Īľšő™°° °°min£Ľ
£®3£©AĶń÷Ķő™°° °°£ģ