题目内容
【题目】综合与实践
数学活动课上,小红画了如图1所示的两个共用直角顶点的等腰直角三角形![]() 与等腰直角三角形
与等腰直角三角形![]() ,其中
,其中![]() ,
,![]() ,连接
,连接![]() ,
,![]() 、
、![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
操作发现:
小红发现了:![]() 、
、![]() 有一定的关系,数量关系为_____________________________;位置关系为_________________.
有一定的关系,数量关系为_____________________________;位置关系为_________________.

类比思考:
如图2,在图1的基础上,将等腰直角三角形![]() 绕点
绕点![]() 旋转一定的角度,其它条件都不变,小红发现的结论还成立吗?请说明理由.(提示:连接
旋转一定的角度,其它条件都不变,小红发现的结论还成立吗?请说明理由.(提示:连接![]() 、
、![]() 并延长交于一点
并延长交于一点![]() )
)
深入探究:
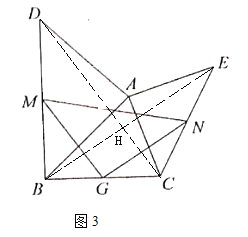
在上述类比思考的基础上,小红做了进一步的探究.如图3,作任意一个三角形![]() ,其中
,其中![]() ,在三角形外侧以
,在三角形外侧以![]() 为腰作等腰直角三角形
为腰作等腰直角三角形![]() ,以
,以![]() 为腰作等腰直角三角形
为腰作等腰直角三角形![]() ,分别取斜边
,分别取斜边![]() 、
、![]() 与边
与边![]() 的中点
的中点![]() 、
、![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,试判断三角形
,试判断三角形![]() 的形状,并说明理由.
的形状,并说明理由.

【答案】操作发现:MG=NG,MG⊥NG;类比思考:MG=NG,MG⊥NG成立,理由见解析;深入探究:△MGN是等腰直角三角形,理由见解析.
【解析】
操作发现:利用SAS判断出△ACD≌△AEB,得出CD=BE,∠ADC=∠ABE,进而判断出∠BDC+∠DBH=90°,即:∠BHD=90°,最后用三角形中位线定理即可得出结论;
类比思考:同操作发现的方法得出MG=NG,最后利用三角形中位线定理和等量代换即可得出结论;
深入探究:同操作发现的方法即可得出结论.
解:操作发现:如图1,连接BE,CD相交于H,
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°
∴∠CAD=∠BAE,
∴△ACD≌△AEB(SAS),
∴CD=BE,∠ADC=∠ABE,
∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,
∴∠BHD=90°,
∴CD⊥BE,
∵点M,G分别是BD,BC的中点,
∴MG∥CD,MG=![]() CD,
CD,
同理:NG∥BE,NG=![]() BE,
BE,
∴MG=NG,MG⊥NG,
故答案为:MG=NG,MG⊥NG;
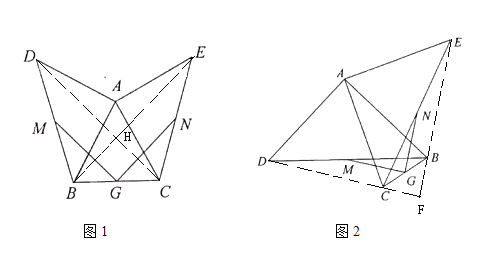
类比思考:MG=NG,MG⊥NG成立,
理由:如图2,连接![]() 、
、![]() 并延长交于一点
并延长交于一点![]()
同操作发现的方法得,MG=NG,
同操作发现的方法得,△ABE≌△ADC,
∴∠AEB=∠ACD,
∴∠CEF+∠ECF=∠AEF-∠AEC+180°-∠ACD-∠ACE=∠ACD-45°+180°-∠ACD-45°=90°,
∴∠DFE=90°,
同操作发现的方法得,MG⊥NG,
∴MG=NG,MG⊥NG;
深入探究:△MGN是等腰直角三角形,
理由:如图3,连接CD,BE相交于点H,
同操作发现的方法得,MG=NG,MG⊥NG,
∴△MGN是等腰直角三角形.
故答案为:操作发现:MG=NG,MG⊥NG;类比思考:MG=NG,MG⊥NG成立,理由见解析;深入探究:△MGN是等腰直角三角形,理由见解析.




