题目内容
如图,在△ABC中,AB=17,AC=5
,∠CAB=45°,点O在BA上移动,以O为圆心作⊙O, 使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
(1)求y与x的函数关系式;
(2)求x的取值范围;
(3)当x为何值时,⊙O与BC、AC都相切?
| 2 |
 使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.(1)求y与x的函数关系式;
(2)求x的取值范围;
(3)当x为何值时,⊙O与BC、AC都相切?
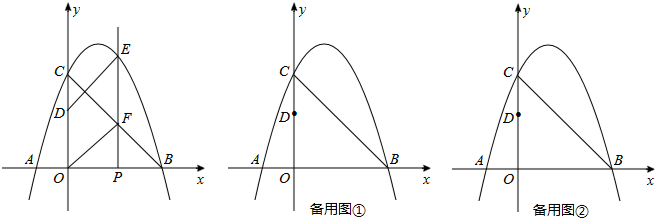
(1)如图①,过点C作CE⊥AB,垂足为E.
在Rt△ACE中,AC=5
,∠CAB=45°,
∴AE=CE=AC•sin45°=5
×
=5.
∴BE=AB-AE=17-5=12,CB=
=
=13.(2分)
∴tanB=
=
.
∵CB切⊙O于点D,
∴OD⊥BC.
又
=
=tanB=
,
∴BD=
x.(4分)
∵S四边形AODC=S△ABC-S△BOD,
∴y=
AB•CE-
BD•OD=
×17×5-
•
x•x=-
x2+
;(6分)
(2)过点C作CF⊥CB交AB于F.
在Rt△BCF中,CF=BC•tanB=13×
=
.
∴x的取值范围是0<x≤
.(9分)
说明:答案为0<x<
不扣分;
(3)当⊙O与BC、AC都相切时,
设⊙O与AC的切点为G,连接OG、OC(如图②),则OG=OD=x.
∵S△AOC+S△BOC=S△ABC,
∴
•5
•x+
•13•x=
•17•5.
∴x=
=
(13-5
).(12分)

在Rt△ACE中,AC=5
| 2 |
∴AE=CE=AC•sin45°=5
| 2 |
| ||
| 2 |
∴BE=AB-AE=17-5=12,CB=
| CE2+EB2 |
| 52+122 |
∴tanB=
| CE |
| EB |
| 5 |
| 12 |
∵CB切⊙O于点D,
∴OD⊥BC.
又
| OD |
| BD |
| x |
| BD |
| 5 |
| 12 |
∴BD=
| 12 |
| 5 |
∵S四边形AODC=S△ABC-S△BOD,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
| 6 |
| 5 |
| 85 |
| 2 |
(2)过点C作CF⊥CB交AB于F.
在Rt△BCF中,CF=BC•tanB=13×
| 5 |
| 12 |
| 65 |
| 12 |
∴x的取值范围是0<x≤
| 65 |
| 12 |
说明:答案为0<x<
| 65 |
| 12 |

(3)当⊙O与BC、AC都相切时,
设⊙O与AC的切点为G,连接OG、OC(如图②),则OG=OD=x.
∵S△AOC+S△BOC=S△ABC,
∴
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 85 | ||
5
|
| 5 |
| 7 |
| 2 |


练习册系列答案
相关题目






 的表达式、隧道的跨度AB和拱高OC.
的表达式、隧道的跨度AB和拱高OC.