题目内容
已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
(1)请求出点A坐标和⊙P的半径;
(2)请确定抛物线的解析式;
(3)M为y轴负半轴上的一个动点,直线MB交⊙P于点D.若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.(先画出符合题意的示意图再求解).

(1)请求出点A坐标和⊙P的半径;
(2)请确定抛物线的解析式;
(3)M为y轴负半轴上的一个动点,直线MB交⊙P于点D.若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.(先画出符合题意的示意图再求解).

(1)∵OA是⊙P的切线,OC是⊙P的割线.
∴OA2=OB×OC,
即OA2=1×4,
∴OA=2,
即点A点坐标是(0,2)
如图1,连接PA,过P作PE⊥CO交OC于E显然,四边形PAOE为矩形,
故PA=OE,
∵PE⊥BC,
∴BE=CE,
又∵BC=3,
∴BE=
,
∴PA=OE=OB+BE=1+
=
,
即⊙P的半径长为
.
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c得:
,
解得:
,
故抛物线的解析式是:y=
x2-
x+2;
(3)根据题意∠OAB=∠ADB,
所以△AOB和△ABD相似有两种情况
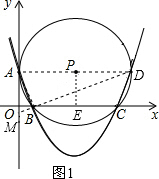
①∠ABD和∠AOB对应,
如图1,此时AD是⊙P的直径则AB=
,AD=5
∴BD=2
,
∵Rt△AMB∽Rt△DAB,
∴MA:AD=AB:BD,
即MA=
=
,
∵Rt△AMB∽Rt△DMA,
∴MA:MD=MB:MA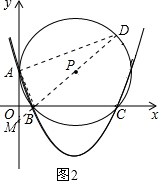
即MB•MD=MA2=
,
②∠BAD和∠AOB对应,
如图2,此时BD是⊙P的直径,所以直线MB过P点
∵B(1,0),P(
,2),
∴直线MB的解析式是:y=
x-
∴M点的坐标为(0,-
),
∴AM=
,
由△MAB∽△MDA,
得MA:MD=MB:MA
∴MB•MD=MA2=
.
∴OA2=OB×OC,
即OA2=1×4,
∴OA=2,
即点A点坐标是(0,2)
如图1,连接PA,过P作PE⊥CO交OC于E显然,四边形PAOE为矩形,
故PA=OE,
∵PE⊥BC,
∴BE=CE,
又∵BC=3,
∴BE=
| 3 |
| 2 |
∴PA=OE=OB+BE=1+
| 3 |
| 2 |
| 5 |
| 2 |
即⊙P的半径长为
| 5 |
| 2 |
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c得:
|
解得:
|
故抛物线的解析式是:y=
| 1 |
| 2 |
| 5 |
| 2 |
(3)根据题意∠OAB=∠ADB,
所以△AOB和△ABD相似有两种情况
①∠ABD和∠AOB对应,
如图1,此时AD是⊙P的直径则AB=
| 5 |
∴BD=2
| 5 |
∵Rt△AMB∽Rt△DAB,
∴MA:AD=AB:BD,
即MA=
| AB•AD |
| BD |
| 5 |
| 2 |
∵Rt△AMB∽Rt△DMA,
∴MA:MD=MB:MA

即MB•MD=MA2=
| 25 |
| 4 |
②∠BAD和∠AOB对应,
如图2,此时BD是⊙P的直径,所以直线MB过P点
∵B(1,0),P(
| 5 |
| 2 |
∴直线MB的解析式是:y=
| 4 |
| 3 |
| 4 |
| 3 |
∴M点的坐标为(0,-
| 4 |
| 3 |
∴AM=
| 10 |
| 3 |
由△MAB∽△MDA,
得MA:MD=MB:MA
∴MB•MD=MA2=
| 100 |
| 9 |


练习册系列答案
相关题目

 ),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
 使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.