题目内容
某地计划开凿一条单向行驶(从正中通过)的隧道,其截面是抛物线拱形ACB,而且能通过最宽3米,最高3.5米的厢式货车.按规定,机动车通过隧道时车身距隧道壁的水平距离和铅直距离最小都是0.5米.为设计这条能使上述厢式货车恰好安全通过的隧道,在图纸上以直线AB为x轴,线段AB的垂直平分线为y轴,建立如图所示的直角坐标系,求抛物线拱形 的表达式、隧道的跨度AB和拱高OC.
的表达式、隧道的跨度AB和拱高OC.
 的表达式、隧道的跨度AB和拱高OC.
的表达式、隧道的跨度AB和拱高OC.设抛物线的表达式为y=ax2+h,
∵图象经过点(1.5,4)和(2,3.5),
∴
,
解之得
.
故抛物线的表达式为y=-
x2+
,
拱高OC即是当x=0时y的值为
米.
当y=0时有-
x2+
=0
解之得x1=
,x2=-
.
即是A、B两点的横坐标,
故可得跨度AB=
米.
∵图象经过点(1.5,4)和(2,3.5),
∴
|
解之得
|
故抛物线的表达式为y=-
| 2 |
| 7 |
| 65 |
| 14 |
拱高OC即是当x=0时y的值为
| 65 |
| 14 |
当y=0时有-
| 2 |
| 7 |
| 65 |
| 14 |
解之得x1=
| ||
| 2 |
| ||
| 2 |
即是A、B两点的横坐标,
故可得跨度AB=
| 65 |

练习册系列答案
相关题目
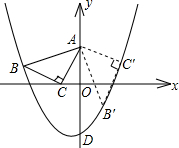 中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).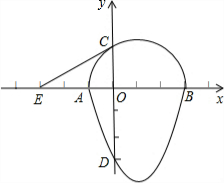
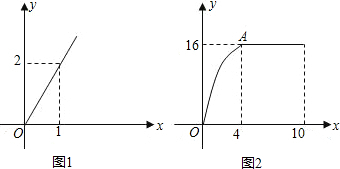 大?
大?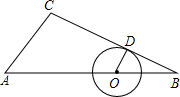 使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.