Question

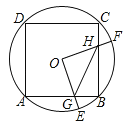
【题目】如图，△ABC中，点O是边AB上一点，以点O为圆心，以OB为半径作⊙O，⊙O恰好与AC相切于点D，连接BD，BD平分∠ABC．

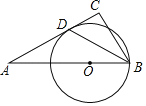
（1）求∠C的度数；

（2）如果∠A＝30°，AD＝2，求线段CD的长度．

Answer 1

【答案】（1）90°；（2）

【解析】

(1)连接OD，∠ADO=90°，由BD平分∠ABC，OB=OD可得OD 与BC间的位置关系，则∠ACB=90°；

(2)得Rt△OAD，由∠A=30°，AD=2，可求出OD、AO的长；根据平行线分线段成比例定理，得结论．

(1)如图，连接OD

∵OD是⊙O的半径，AC是⊙O的切线，点D是切点，

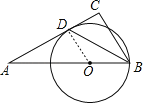
∴OD⊥AC

∵OD=OB，

∴∠ODB=∠OBD，

又∵BD平分∠ABC，

∴∠OBD=∠CBD

∴∠ODB=∠CBD

∴OD∥CB，

∴∠C=∠ADO=90°；

(2)在Rt△AOD中，∠A=30°，AD=2，

∴，，

∵OD∥CB，

∴，

即，

∴CD=．