题目内容
(10分)如图1,O为正方形ABCD的中心,

分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.

分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转
 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).(1)探究AE1与BF1的数量关系,并给予证明;
(2)当
 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.解:(1)AE1=BF1,证明如下:

∵O为正方形ABCD的中心,∴OA=OB=OD,∴OE=OF
∵△E1OF1是△EOF绕点O逆时针旋转 角得到,∴OE1=OF1。
角得到,∴OE1=OF1。
∵∠AOB=∠EOF=900,∴∠E1OA=900-∠F1OA=∠F1OB
 OE1=OF1
OE1=OF1
在△E1OA和△F1OB中, ∠E1OA=∠F1OB,∴△E1OA≌△F1OB (SAS)
OA=OB
∴AE1=BF1。
(2)取OE1中点G,连接AG。
∵∠AOD=900, =30° ,∴∠E1OA=900-
=30° ,∴∠E1OA=900- =60°。
=60°。
∵OE1=2OA,∴OA=OG,∴∠E1OA=∠AGO=∠OAG=60°。
∴ AG=GE1,∴∠GAE1=∠GE1A=30°。∴∠E1AO=90°。
∴△AOE1为直角三角形。

∵O为正方形ABCD的中心,∴OA=OB=OD,∴OE=OF
∵△E1OF1是△EOF绕点O逆时针旋转
 角得到,∴OE1=OF1。
角得到,∴OE1=OF1。∵∠AOB=∠EOF=900,∴∠E1OA=900-∠F1OA=∠F1OB
 OE1=OF1
OE1=OF1在△E1OA和△F1OB中, ∠E1OA=∠F1OB,∴△E1OA≌△F1OB (SAS)
OA=OB
∴AE1=BF1。
(2)取OE1中点G,连接AG。
∵∠AOD=900,
 =30° ,∴∠E1OA=900-
=30° ,∴∠E1OA=900- =60°。
=60°。∵OE1=2OA,∴OA=OG,∴∠E1OA=∠AGO=∠OAG=60°。
∴ AG=GE1,∴∠GAE1=∠GE1A=30°。∴∠E1AO=90°。
∴△AOE1为直角三角形。
略

练习册系列答案
相关题目
 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)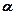 (
(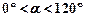 且
且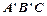 ,
,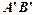 边经过点B时,求旋转角
边经过点B时,求旋转角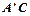 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥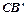 边于点E,联结BE.
边于点E,联结BE.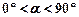 时,设
时,设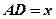 ,
,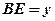 ,求
,求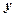 与
与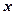 之间的函数解析式及定义域;
之间的函数解析式及定义域;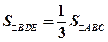 时,求
时,求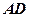 的长.
的长. 



 ,则△ABC的周长等于____________
,则△ABC的周长等于____________