题目内容
如图,在△ABC中,∠C=90°,AD所在直线是∠BAC的对称轴,DE⊥AB于E,点F在AC上,BD=DF.
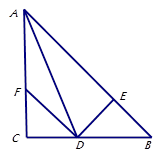
求证:(1)DC=DE;
(2)CF="EB."

求证:(1)DC=DE;
(2)CF="EB."
(1)证明见解析;(2)证明见解析.
试题分析:(1)根据角平分线上的点到角的两边的距离相等证明即可;
(2)利用“边角边”证明△BDE和△FDC全等,再根据全等三角形对应边相等证明即可.
试题解析:(1)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DE=DC;
(2)在△BDE和△FDC中,
∵BE=CF,∠C=∠DEB=90°,DE=DC,
∴△BDE≌△FDC(SAS),
∴BD=DF.
考点: 1.角平分线的性质;2.全等三角形的判定与性质.

练习册系列答案
相关题目
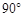 ,周长为10cm,斜边上的中线CD=2cm,则Rt⊿ABC的面积为 。
,周长为10cm,斜边上的中线CD=2cm,则Rt⊿ABC的面积为 。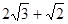 和
和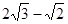 ,则矩形的对角线的长为 。
,则矩形的对角线的长为 。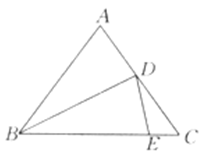
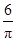 cm,一只蚂蚁从点
cm,一只蚂蚁从点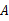 爬到点
爬到点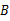 处吃食,要爬行的最短路程是( )
处吃食,要爬行的最短路程是( )