题目内容
【题目】阅读下列材料:
数学课上,老师出示了这样一个问题:
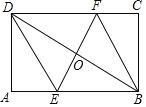
如图,菱形![]() 和四边形
和四边形![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
求证:![]() ;
;
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察分析,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察分析,发现图中有等腰三角形”;
小伟:“利用等腰三角形的性质就可以推导出![]() ”.
”.
……
老师:“将原题中的条件‘![]() ’与结论‘
’与结论‘![]() ’互换,即若
’互换,即若![]() ,则
,则![]() ,其它条件不变,即可得到一个新命题”.
,其它条件不变,即可得到一个新命题”.
……
请回答:
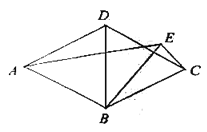
(1)在图中找出与线段![]() 相关的等腰三角形(找出一个即可),并说明理由;
相关的等腰三角形(找出一个即可),并说明理由;
(2)求证:![]() ;
;
(3)若![]() ,则
,则![]() 是否成立?若成立,请证明;若不成立,请说明理由.
是否成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先利用菱形的性质,得出![]() 是等边三角形,再利用等边三角形的性质,即可解答
是等边三角形,再利用等边三角形的性质,即可解答
(2)设![]() ,根据菱形的性质得出
,根据菱形的性质得出![]() ,由(1)可知
,由(1)可知![]() ,即可解答
,即可解答
(3)连接![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,连接
,连接![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,首先证明
,首先证明![]() ,再根据全等三角形的性质得出
,再根据全等三角形的性质得出![]() 是等边三角形,然后再证明
是等边三角形,然后再证明![]() ,即可解答
,即可解答
(1)![]() 是等腰三角形;
是等腰三角形;
证明:∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
∵![]() ,∴
,∴![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
(2)设![]() .
.
∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
∴![]() .
.
由(1)知,![]() ,同理可得:
,同理可得:![]() .
.
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() .
.
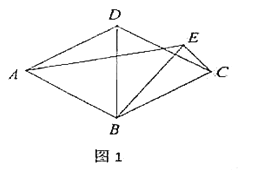
(3)成立;
证明:如图2,连接![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,连接
,连接![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() (ASA),
(ASA),
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,
∵![]() ,∵
,∵![]() ,∴
,∴![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

【题目】某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下:(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
+15 | -8 | +6 | +12 | -4 | +5 | -10 |
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.1升,问共耗油多少升?