Question

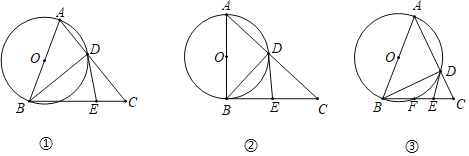
【题目】如图，在等边三角形的，边上分别任取一点，，且，、相交于点．下列四个结论：①若，则；②若，，则；③；④若，则的最小值为，其中正确的是（ ）

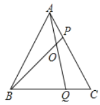
A.①②④B.①③④C.②③④D.①②③

Answer 1

【答案】B

【解析】

过点P作PD∥BC交AQ于点D，证出，即可判断①；过点B作BE⊥AC于E，利用勾股定理求出PE，即可判断②；利用SAS即可证出△ABP≌△CAQ，然后证出△BPA∽△APO，列出比例式，利用等量代入即可判断③；以BA为边作等边△NAB，连接CN，利用四点共圆、锐角三角函数即可判断④．

解：∵△ABC为等边三角形

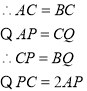
，AP：AC=1:3

过点P作PD∥BC交AQ于点D

∴

∴

∴CQ=3PD

∴BQ=6PD

∴，故①正确；

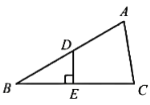
过点B作BE⊥AC于E，

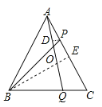
∴CE=AC=BC= 4

根据勾股定理可得BE=

PE=

∴CP=CE＋PE=5或CP=CE－PE=3，故②错误；

∵△ABC为等边三角形

∴AB=CA，∠BAP=∠ACQ

在△ABP和△CAQ中

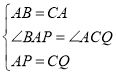
∴△ABP≌△CAQ

∴∠PBA =∠PAO，BP=AQ

∵∠BPA=∠APO

∴△BPA∽△APO

∴

∴，

∴，故③正确；

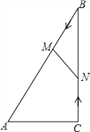
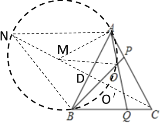
以BA为边作等边△NAB，连接CN

∴∠NAB=∠NBA=60°，NA=NB

∵∠PBA=∠QAC

∴∠NAO＋∠NBO=∠NAB＋∠BAQ＋∠NBA＋∠PBA

=60°＋∠BAQ＋60°＋∠QAC

=120°＋∠BAC

=180°

∴点N、A、O、B四点共圆，且圆心即为等边△NAB的中心M，设CM与圆M的交点O′，CO′即为CO的最小值

∵NA=NB，CA=CB

∴CN垂直平分AB

∴∠MAD=∠ACM=30°

∴∠MAC=∠MAD＋∠BAC=90°

在Rt△MAC中，AC=3，

∴MA=AC·tan∠ACM=，CM=2AM=2

∴MO′=MA=

∴CO′=CM－MO′=

即CO的最小值为，故④正确．

综上：正确的有①③④

故选B．