题目内容
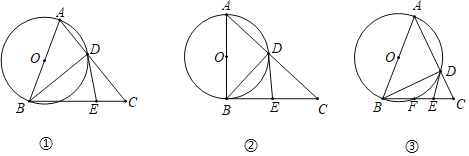
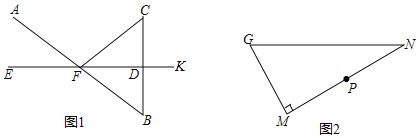
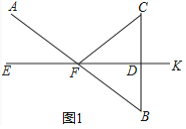
【题目】（1）如图1，已知EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF．求证：∠AFE=∠CFD．
（2）如图2，在Rt△GMN中，∠M=90°，P为MN的中点．
①用直尺和圆规在GN边上求作点Q，使得∠GQM=∠PQN（保留作图痕迹，不要求写作法）；
②在①的条件下，如果∠G=60°，那么Q是GN的中点吗？为什么？
【答案】(1)证明见解析；（2）①作图见解析；②结论：
是
的中点．理由见解析.
【解析】
（1）只要证明FC=FB即可解决问题；
（2）①作点P关于GN的对称点P′，连接P′M交GN于Q，连接PQ，点Q即为所求．
②结论：Q是GN的中点．想办法证明∠N=∠QMN=30°，∠G=∠GMQ=60°，可得QM=QN，QM=QG；
（1）证明：如图1中，
垂直平分线段
，
，
，
，
．
（2）①作点
关于的对称点
，连接
交于，连接
，点即为所求．
理由：
垂直平分
，
，
，
，
，
点即为所求．
②结论：是的中点．
理由：设交于
．
，
，
，
，
，
，
，
，
，
，
，
，
，
，
是的中点．
练习册系列答案
阅读快车系列答案
相关题目
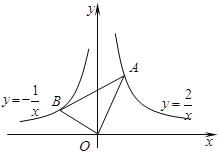
【题目】有这样一个问题：探究函数y＝
的图象与性质．小彤根据学习函数的经验，对函数y＝的图象与性质进行了探究．
下面是小彤探究的过程，请补充完整：
(1)函数y＝的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ；
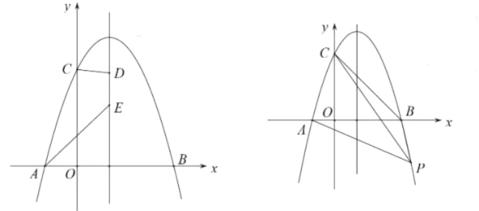
(3)如图所示，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；
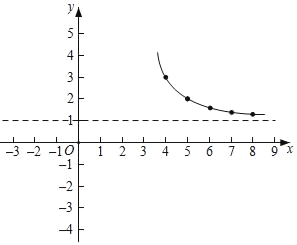
(4)观察图象，写出该函数的一条性质 ；
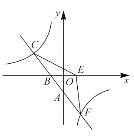
(5)若函数y＝的图象上有三个点A(x1，y1)、B(x2，y2)、C(x3，y3)，且x1＜3＜x2＜x3，则y1、y2、y3之间的大小关系为 ；
