题目内容
【题目】小张骑自行车匀速从甲地到乙地，在途中休息了-段时间后，仍按原速行驶他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段AB所示，
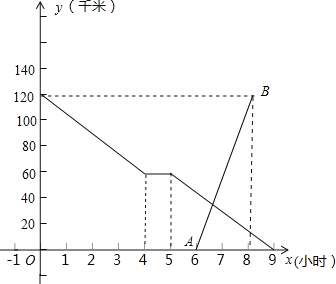
(1)小李到达甲地后，再经过 小时小张到达乙地；小张骑自行车的速度是 千米/小时；
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇，则他出发的时间x应在什么范围?(直接写出答案)
【答案】（1）1，15；（2）
；（3）
.
【解析】
（1）由图象看出所需时间和速度；
（2）先求出小李的速度，然后根据图象可以得出结论；
（3）若在休息期间相遇直线AB必须与在4<x<5的线段相交，画出图形，求出取值范围．
解：（1）根据题意可知，小李到达甲地后，再经过1小时小张到达乙地；
由
，得
小张骑自行车的速度是：
千米/小时；
故答案为：1，15；
（2）根据题意，小李从乙地到甲地，用两小时走完了120千米，
∴小李的速度为：
千米/小时，
∴小李距乙地的距离y与时间x之间的函数关系为：；
（3）若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇，则如图：
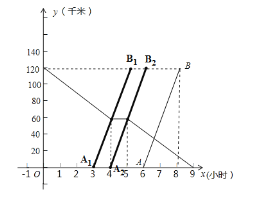
∵小张休息时走过的路程是：15×4=60（千米），
∴小李应走的路程是：120-60=60（千米），
∴小李走60千米所需的时间是：60÷60=1（小时）；
若相遇时间在第4小时，则小李出发时间为第3小时；
若相遇时间在第5小时，则小李出发时间为第4小时；
∵第4小时和第5小时不算小张休息时间，
∴x的取值范围是：.
【题目】某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完．该公司的年产量为6000件，若在国内市场销售，平均每件产品的利润与国内销售量
的关系如下表：
销售量 |
|
|
单件利润（元） |
|
|
若在国外销售，平均每件产品的利润与国外的销售数量
的关系如下表：
销售量 |
|
|
单件利润（元） | 100 |
|
（1）用的代数式表示为：=；
（2）该公司每年国内、国外的销售量各为多少时，可使公司每年的总利润为60万元？
