题目内容
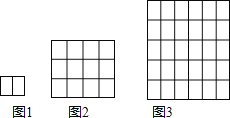
【题目】这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用_____木块才能把第四次所铺的完全围起来.
【答案】34块
【解析】
观察图形发现:若要将前一个图形包起来,上下各需要添一层,左右各需添一层,结合图1两块木块可以得出图n需要木块数为[1+(n﹣1)×2]×[2+(n﹣1)×2],求出图4图5所需木块数,二者相减即可得出结论.
解:若要将前一个图形包起来,上下各需要添一层,左右各需添一层,
即图1木块个数为1×2,图2木块个数为(1+2)×(2+2),图3木块个数为(1+2×2)×(2+2×2),…,图n木块个数为[1+(n﹣1)×2]×[2+(n﹣1)×2].
由上面规律可知:图4需要木块个数为(1+3×2)×(2+3×2)=56(块),图5需要木块个数为(1+4×2)×(2+4×2)=90(块),
故铺第5次时需用90﹣56=34块木块才能把第四次所铺的完全围起来.
故答案为:34块.

练习册系列答案
相关题目