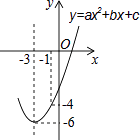题目内容
【题目】如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 . 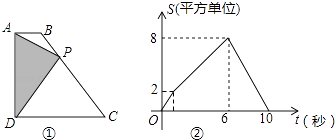
【答案】5
【解析】解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD= ![]() ×AD×DC=8,
×AD×DC=8,
∴AD=4,
又∵S△ABD= ![]() ×AB×AD=2,
×AB×AD=2,
∴AB=1,
当P点运动到BC中点时,BP=PC,
如图,作PQ⊥AB于点Q,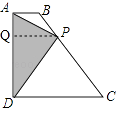
∴AB∥PQ∥CD,
∴PQ为梯形ABCD的中位线,
则PQ= ![]() (AB+CD),
(AB+CD),
∴△PAD的面积= ![]() ×
× ![]() (AB+CD)×AD=5,
(AB+CD)×AD=5,
故答案为:5.
由函数图象上的点(6,8)、(10,0)的实际意义可知AB+BC、AB+BC+CD的长及△PAD的最大面积,从而求得AD、CD的长,再根据点P运动到点B时得S△ABD=2,从而求得AB的长,最后根据等腰三角形的中位线定理可求得当P运动到BC中点时,△PAD的面积.

练习册系列答案
相关题目
【题目】在股市交易中,每买、卖一次需付交易款的千分之七点五作为交易费用,某投资者以每股10元的价格买入某股票1 000股,下表为第一周内每日该股票的涨跌情况(单位:元).
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2 | +1.5 | -0.5 | -4.5 | +2.5 |
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)若该投资者在星期五收盘前将股票全部卖出,他的收益情况如何?